

|
|
УДК 550.383:550.385
Космические исследования. 2001. Т. 39. № 6. с. 563-
596.Cosmic Res., V. 39. No. 6. р. 527- 558, 2001.
ГЕОКОРОНА ГОРЯЧЕЙ ПЛАЗМЫ
А. С. Ковтюх
Научно-исследовательский институт ядерной физики
им. Д. В. Скобельцына, МГУ
Поступила в редакцию
07.02.2001 г.В данном обзоре рассматриваются основные результаты экспериментальных и теоретических исследований (а также численного моделирования) распределений, состава и динамики частиц горячей плазмы в геомагнитосфере. Основное внимание уделяется кольцевому току и плазменному слою магнитосферного хвоста, играющим в физике магнитосферы ключевую роль. Обосновывается целостность (единство) системы “ внешний радиационный пояс - кольцевой ток - ближний плазменный слой” (концепция геокороны горячей плазмы). С позиций такой концепции рассмотрены физические процессы и теории, предложенные для объяснения структуры и динамики горячей магнитосферной плазмы. Акцентируются дискуссионные вопросы и нерешённые актуальные задачи.
Основными резервуарами горячей магнитосферной плазмы являются кольцевой ток (КТ) в геомагнитной ловушке и плазменный слой (ПС) магнитосферного хвоста. КТ и ПС находятся в областях с различной топологией магнитного поля и формируются различными динамическими процессами. Поэтому в существующих учебниках и монографиях КТ и ПС принято рассматривать как принципиально разные плазменные структуры.
Однако в результатах экспериментальных и теоретических исследований последних лет обнаруживаются тесные взаимосвязи и, во многих отношениях, - единство этих структур. Основу для такого единства можно было усмотреть
a priori в следующих обстоятельствах: ПС непосредственно примыкает к КТ; ПС является основным поставщиком плазмы в КТ; КТ и ПС питаются из одних и тех же источников (солнечного ветра и ионосферы).Основная цель данного обзора - уточнить основные понятия, относящиеся к ионным компонентам КТ и ПС, и дать целостную картину их динамики. Поскольку библиография публикаций по затронутым вопросам достигает нескольких тысяч статей, для краткости здесь приводятся ссылки только на наиболее важные или типичные работы; принятая в таких случаях оговорка (см., например) здесь опускается.
Сначала мы рассмотрим КТ и ПС по отдельности, выделяя присущие им специфические особенности, а затем установим взаимосвязи между распределениями ионов КТ и ПС и рассмотрим их как единое плазменное образование. В последнем разделе с позиций такого единства обсуждаются результаты анализа экспериментов и основные механизмы, предложенные для объяснения структуры и динамики КТ и ПС.
К важнейшим характеристикам распределений горячей плазмы в планетарной магнитосфере относятся ионный состав, форма энергетических спектров и питч-угловые распределения. Они зависят от расстояния точки наблюдения до Земли, местного времени (LT), уровня и характера геомагнитной активности, фазы солнечного цикла и вспышечной активности на Солнце, условий в межпланетном пространстве и др. факторов.
Планетарный КТ лежит в основе механизма геомагнитных бурь. Введение в геофизику кольцевого тока [1] было продиктовано тем обстоятельством, что во время бурь горизонтальная составляющая геомагнитного поля на низких и средних широтах понижается, причём на данной геомагнитной широте величина этого понижения поля практически не зависит от местного времени точки наблюдения (такая зависимость появляется только в самом начале бури и быстро исчезает). Такой магнитный эффект отвечает циркулирующему вокруг Земли замкнутому электрическому току, направленному на запад. Силу этого тока принято оценивать по величине Dst - усреднённой по долготе горизонтальной составляющей возмущения магнитного поля на низких и средних широтах: во время слабых и умеренных бурь Dst понижается до - 30¸ 100 нТ, а во время гигантских бурь - до - 200¸ 300 нТ и более.
“Спокойный” КТ можно отождествить с магнитным дрейфом заряженных частиц с E > 0.1 МэВ в геомагнитной ловушке, составляющих радиационные пояса (РП): электроны РП дрейфуют на восток, а протоны и другие положительные ионы - на запад и в целом РП можно рассматривать как направленный на запад кольцевой ток; связанное с ним понижение наземного магнитного поля на низких и средних широтах (- 10¸ 20 нТ) приближается к наблюдаемым отклонениям от чисто земного магнетизма. Однако во время активной (главной) фазы бури депрессия магнитного поля в сердцевине ловушки увеличиваются в десятки раз, а отвечающий РП кольцевой ток усиливается всего в несколько раз или даже уменьшается. Этот парадокс разрешился после открытия пояса частиц с E < 100 кэВ [2].
Вблизи экваториальной плоскости и на средних геомагнитных широтах распределения ионов КТ изучались по данным ИСЗ OGO-3 [2- 4], ATS-5 [5], Explorer-45 [6- 12], Молния-1 [13- 17], ATS-6 [18], GEOS-1 [19- 21], GEOS-2 [20- 22], Прогноз-7 [23, 24], ISEE-1 [25, 26], SCATHA [27, 28], AMPTE/CCE [29- 46], Горизонт-21 [47- 51], CRRES [52- 59], Горизонт-35 [60- 65], Polar [66] и др.
В результате этих экспериментов было установлено, что во время типичных бурь основной (~ 80¸ 90%) вклад в КТ вносят ионы с Е/Qi ~ 10¸ 100 кэВ, где Qi - заряд иона по отношению к заряду протона [6, 12, 32], а во время больших бурь верхняя граница этого диапазона может смещаться до 200¸ 300 кэВ [35]. Относительный вклад электронов в давление (плотность энергии) и магнитный эффект КТ во время слабых и умеренных бурь не превышает 25% [2], а во время сильных бурь этот вклад уменьшается до 10% и меньше.
Радиальные профили потоков ионов КТ имеют широкий максимум, который приходится на L = 5.5¸ 6.0 (L - параметр Мак-Илвайна) в спокойных условиях и на L = 2.5¸ 5.0 - во время бурь (чем больше max½ Dst½ , тем ближе КТ подходит к Земле). Спокойный КТ имеет пологую внешнюю и более крутую внутреннюю кромку, причём середина внутренней кромки КТ (L ~ 4.5) примерно совпадает с усредненным по LT положением плазмопаузы. Во время главной фазы бури внутренняя кромка КТ становится значительно более крутой и узкой, по-прежнему совпадая с положением плазмопаузы [4, 6, 7, 10, 11, 18, 57, 58].
Спокойный ионный КТ состоит в основном (на ~ 80%) из протонов. По усредненным на L = 5¸ 7 данным, в спокойные периоды средние парциальные концентрации ионов H+, O+, N+, He+, He2+, O2+ и (C6+ + O6+) с E/Qi = 10¸ 315 кэВ составляют ~ 80, 14, 3, 3, 0.5, 0.3 и 0.02% соответственно [32]. В периоды магнитных активизаций КТ обогащается ионами с Mi > 1 (Mi - масса ионов по отношению к массе протона), причём доля ионов O+ приближается к доле протонов или даже превышает её (в зависимости от характера и мощности бури). После ионов H+ и O+ в порядке важности идут N+, He+, He2+ и т.д. Так, во время главной фазы слабых и умеренных бурь (c max½ Dst½ ~ 50¸ 160 нТ) средние парциальные концентрации ионов H+ и (N,O)+ для диапазона E/Qi = 10¸ 315 кэВ в сердцевине КТ (на L ~ 3¸ 5) составляют ~ 62 и ~ 35%, а средние парциальные плотности энергии ~ 69% и ~ 27% соответственно [32]. Во время трёх суббурь временные вариации AE-индекса и плотности энергии ионов O+ c E = 50¸ 426 кэВ на L = 5¸ 6 хорошо соответствовали друг другу и значительно отличались от вариаций плотности энергии ионов H+ c E = 20¸ 426 кэВ [52].
Для изучения механизмов инжекции и других процессов, связанных с динамикой КТ наиболее подходящей является геосинхронная орбита (ГСО) - круговая орбита в географической экваториальной плоскости с радиусом 6.62 RE или ~ 40 тыс. км (RE - радиус Земли) и периодом 24 ч, которая пересекает граничные дрейфовые оболочки и область квазизахвата частиц. На ГСО обычно функционируют одновременно несколько спутников. В дальнейшем под областью ГСО мы будем понимать интервал L ~ 6¸ 7 вблизи экваториальной плоскости.
В области ГСО ионный состав горячей плазмы сильно варьирует даже во время небольших магнитных возмущений [19- 21, 25, 30, 47, 48] и эффект обогащения КТ ионами O+ прослеживается в широком диапазоне (от нескольких кэВ до нескольких сотен кэВ), причём во время отдельных суббурь этот эффект наиболее значителен при энергиях в несколько сотен кэВ [53]. Очень сложные и разнообразные вариации, зависящие от характера и уровня геомагнитной активности, испытывают на ГСО зарядовые распределения ионов группы СNO (Qi = + 2¸ 6) с E/Qi ~ 40¸ 70 кэВ (локальный максимум в спектрах); эти распределения резко изменяются в периоды магнитных активизаций, но очень быстро, гораздо быстрее чем потоки и энергетические спектры, восстанавливаются к равновесному состоянию [47, 48]. В зарядовых распределениях ионов кислорода с E/Qi = 1¸ 300 кэВ в области ГСО чётко выделяются компоненты O+ и O6+: с ростом Kp потоки их резко увеличиваются, а потоки ионов с промежуточными зарядами изменяются слабо [32].
При E/Qi ~ 1¸ 20 кэВ потоки протонов на L > 5 практически всегда доминируют [20, 25, 30]. В спокойные периоды и во время умеренных бурь потоки протонов во внешней части КТ доминируют в более широких диапазонах: при E/Qi ~ 40¸ 130 кэВ [48, 60] и E ~ 0.1¸ 300 кэВ [66]. Как правило, потоки ионов O+ и He+ с E < 10¸ 20 кэВ могут превышать протонные только на внутренней (L < 4) кромке КТ [23, 24], что свидетельствует о более глубоком (по сравнению с протонами) проникновении этих ионов в геомагнитную ловушку во время бурь. Во внешней области ловушки (L > 5) потоки ионов O+ КТ могут превышать протонные только во время очень сильных бурь [27, 67].
В отличие от потоков, концентрации и плотности энергии ионов O+ с E < 10¸ 20 кэВ могут превышать протонные в несколько раз, а на внутренней кромке КТ - в некоторых случаях даже на порядок величины [18, 23, 25]. Однако при бó льших энергиях такое превышение и доминирование в полной энергии КТ ионов O+ наблюдалось только во время гигантских (с max½ Dst½ ~ 300 нТ) бурь [35, 45].
С ростом солнечной активности парциальные концентрации ионов O+ и Hе+ с E/Qi = 1¸ 16 кэВ в области ГСО увеличиваются, причём концентрация ионов O+ возрастает более чем на порядок величины и хорошо коррелирует с потоком солнечного ультрафиолета [21, 26].
В спокойные периоды энергетические спектры ионов на L < 5 имеют глубокий минимум (провал) при E/Qi ~ 20¸ 100 кэВ и максимум при E/Qi ~ 100 кэВ (эта величина зависит от L), а при бó льших энергиях потоки монотонно уменьшаются с ростом энергии. Указанный провал в ионных спектрах сильнее всего выражен на L ~ 4, а с увеличением L он смещается в сторону меньших энергий и постепенно вырождается; во время бурь он частично или полностью заполняется: потоки ионов таких энергий возрастают наиболее значительно - на 1¸ 2 порядка величины [6, 7, 10, 32]. При меньших энергиях (~ 1¸ 25 кэВ) ионные спектры имеют в геомагнитной ловушке очень сложную быстро меняющуюся во время бурь и суббурь форму, причём спектры He2+ и других ионов солнечного происхождения обычно обрезаны снизу при энергии в несколько кэВ [25].
Типичные питч-угловые распределения (ПУР) ионов КТ имеют форму "пончика" (с максимумом при a 0 = 90o) и в районе ГСО близки к изотропным; с уменьшением L и/или увеличением E анизотропия таких ПУР увеличивается [11, 30]. ПУР ионов O+ с E ~ 10¸ 20 кэВ часто имеют форму "сигары" или "коника" (с максимумом при a 0 ~ 0) [30], а во время суббурь такие ПУР ионов O+ наблюдались (в дневные часы LT) при энергиях до нескольких сотен кэВ [37].
ПС - слой горячей плазмы, который разделяет северную и южную доли магнитосферного хвоста и замыкается вокруг Земли в области между внешней границей ловушки и магнитопаузой. Принято идентифицировать ПС в границах области, в которой отношение плотности энергии плазмы к плотности энергии магнитного поля b > 0.1.
Распределения ионов в ПС и в примыкающих к нему периферийных областях магнитосферы изучались по данным ИСЗ
IMP-7 и IMP-8 [68, 69], Прогноз-7 [24], ISEE-1 [25, 70- 77], ISEE-2 [72, 78, 79], ISEE-3 [79- 81], AMPTE/CCE [32, 40, 82- 86], AMPTE/IRM [32, 82, 84, 86- 90], CRRES [52, 53], Geotail [79, 91- 93], Ulysses [94], Galileo [95], ИНТЕРБОЛ [96, 97] и др.В результате этих экспериментов было установлено, что толщина ПС составляет ~ 2¸ 4 RE, ширина (диаметр магнитосферного хвоста) ~ 25¸ 40 RE, длина (вдоль линии Солнце-Земля) ~ 30¸ 200 RE , типичное среднее значение индукции магнитного поля в ПС ~ 25 нТ. При рассмотрении приэкваториальных областей магнитосферы в качестве координаты мы будем использовать параметр r - расстояние (в RE) точки наблюдения до центра Земли (в области дипольного поля r = L).
Как и в КТ, в составе спокойного ПС ионы H
+ доминируют, причём с удалением точки наблюдения от сердцевины ПС к долям хвоста парциальная концентрация протонов уменьшается [76]. Для диапазона E/Qi = 0.1¸ 17 кэВ парциальные концентрации ионов O+, He2+ и He+ в сердцевине ближнего ПС составляют ~ 2¸ 7%, ~ 0.3¸ 4.4% и < 0.5% [71].Ионный состав ближнего ПС непостоянен и может существенно меняться не только во время суббурь, но и в относительно спокойные периоды [84]. Во время среднестатистической суббури парциальные концентрации ионов кислорода и углерода с
Qi £ 2 на r ~ 8¸ 9 увеличиваются в ~ 3 раза, а ионов с Qi ³ 3 - уменьшаются в ~ 2 раза [32]. На r = 7¸ 9 коэффициент корреляции плотности энергии ионов с E/Qi ~ 1¸ 300 кэВ с AE-индексом составляет ~ 0.7 для O+ и ~ 0.4 для H+ [85].Наиболее значительны суббуревые увеличения концентрации ионов O
+, особенно в диапазоне E/Qi ~ 1¸ 20 кэВ, где вклад O+ в полную концентрацию ионов достигает ~ 50% и более [71]. При бó льших энергиях вклад O+ в ионный состав ПС обычно менее значителен: парциальная концентрация ионов O+ с E/Qi = 25¸ 230 кэВ на r = 15 увеличивается от 3.0 до 9.1% [32]. Однако во время некоторых суббурь в ближнем ПС наблюдались значительные увеличения парциальной концентрации ионов O+ (иногда она приближалась к парциальной концентрации ионов H+ и даже немного превышала последнюю) и для диапазона E/Qi от нескольких десятков до нескольких сотен кэВ [86, 93]. По отношению к потокам H+ увеличиваются также потоки He+ в диапазоне E/Qi = 30¸ 230 кэВ [86].Таким образом, во время суббурь ПС обогащается O
+ и другими ионосферными ионами. Однако суббуревые эффекты кратковременны, с увеличением r влияние ионосферного источника на ионный состав ПС постепенно уменьшается и на достаточно больших расстояниях от Земли (r ~ 28¸ 45) состав горячей плазмы ПС в среднем примерно такой же как в солнечном ветре [68].С ростом уровня геомагнитной активности концентрация ионов увеличивается вблизи полуночного меридиана ближнего ПС [79] и уменьшается на его флангах [74].
Распределения ионов как в ближних [32], так и в достаточно удаленных от Земли [95] областях ПС неравновесны. В ближнем ПС спектры ионов имеют максимум при
Em/Mi ~ 4¸ 6 кэВ в спокойные периоды и при Em/Mi ~ 10¸ 15 кэВ во время геомагнитных возмущений [40]. При бó льших энергиях спектры ионов ближнего ПС имеют близкую к степеннó й форму с показателем g = 5¸ 7 [69, 96]. Для спокойного ПС на r ~ 15 спектры ионов H+, He+, He2+ и O+ в диапазоне E/Qi ~ 10¸ 230 кэВ имеют примерно одинаковый наклон, а во время суббурь степеннó й хвост всех спектров становится жёстче, причём для ионов He+ и O+ это изменение больше, чем для ионов H+ и He2+ [86].ПУР ионов горячей плазмы в сердцевине ПС, а также в долях хвоста, в среднем практически изотропны [25, 76]. Однако на фоне изотропных потоков у границ ПС наблюдаются направленные вдоль магнитного поля пучки, состоящие в основном из ионов H
+ и O+ [25]. Аналогичные пучки меньшей интенсивности наблюдаются в долях магнитосферного хвоста, причём здесь доминируют ионы O+ [25, 40]. Динамика ионных пучков в магнитосферном хвосте имеет импульсный характер и с ростом геомагнитной активности вероятность наблюдения ионных пучков увеличивается (особенно для ионов O+).Основные наши аргументы в пользу генетического (а во многом и фактического) единства ближнего ПС, КТ и внешнего РП основаны на взаимосвязях их пространственно-энергетических распределений. Поскольку принципиальные различия между распределениями и динамикой ионов КТ и более энергичными ионами внешнего РП проявляются только во время суббурь и на главной фазе бурь, для магнитно-спокойных периодов все ионы с E/Qi > 10 кэВ во внешней части геомагнитной ловушки мы будем относить далее к КТ.
Основные параметры пространственных и питч-угловых распределений ионов КТ во внешней области ловушки (показатели анизотропии, радиального хода, суточного хода на ГСО и т. д.) отражают структуру магнитного и электрического полей в ловушке и определяются формой энергетических спектров ионов у внешней границы ловушки.
Наиболее полное решение вопроса о форме спектров ионов КТ и законах их подобия для различных ионных компонентов было получено в результате анализа данных ИСЗ Injun-4, Injun-5, 1968-26B, OV1-19, Explorer-45, 1972-076B, Молния-1, ATS-6, Молния-2, Geos-1, Geos-2, ISEE-1, SCATHA, AMPTE/CCE, Горизонт-21, Viking, Akebono, CRRES, Горизонт-35 и ETS-VI в [99- 103]. Анализ проводился методом “ спектрометра с магнитным парусом” [98], в котором поле геомагнитной ловушки служит дополнительным магнитным анализатором. Этот метод позволяет существенно расширить информацию об энергетических спектрах ионов КТ, привлекая к анализу радиальные профили потоков и их отношений для различных ионных компонентов.
Для квазистационарных условий получены аналитические взаимосвязи между энергетическими спектрами ионов, радиальными профилями их потоков, спектральных параметров и отношений потоков для различных ионных компонентов. Эти взаимосвязи чётко прослеживаются по экспериментальным данным, что позволяет систематизировать результаты измерений и на этой основе надёжно определить основные параметры ионных спектров. При переходе от E к m ионов спектры приобретают инвариантную форму, которая не зависит от L и очень удобна для анализа (m - первый адиабатический инвариант движения частиц).
Установлено, что вблизи экваториальной плоскости ловушки энергетические спектры основных ионных компонентов (H+, He+, He2+ и группы CNO) в спокойных условиях имеют максимум при m m/x i » 0.5 ± 0.2 кэВ/нТ, близкую к экспоненциальной форму с E0/B0x i = m 0/x i = 0.35 ± 0.25 кэВ/нТ при m m/x i < m /x i < m b/x i и степенную форму c показателем g = 4.7 ± 2.2 при m /x i > m b/x i = 1.4 ± 0.8 кэВ/нТ (x i - коэффициент подобия спектров). При 0.1 < m /x i < 0.5 ± 0.2 кэВ/нТ в ионных спектрах имеется провал, который заполняется частицами буревого КТ.
Разброс этих параметров связан в основном с методическими и статистическими погрешностями экспериментов (для протонных спектров получены более точные параметры: m m » 0.55 ± 0.10 кэВ/нТ, m 0 = 0.31 ± 0.11 кэВ/нТ, m b = 1.16 ± 0.29 кэВ/нТ и g = 4.25 ± 0.75), а также - с некоторым различием солнечных и геофизических условий. Для мгновенных значений параметров ионных спектров m b » g m 0 (это соотношение отвечает плавному, без излома, переходу экспоненциального участка спектра в степенной хвост). Во время продолжительных спокойных периодов показатели степеннó го хвоста g в спектрах различных ионных компонентов имеют близкие друг к другу значения, а во время бурь значения этого параметра могут расходиться более существенно.
От минимума к максимуму солнечной активности коэффициент подобия спектров x i изменяется от Mi к Qi , экспоненциальный участок спектров смягчается и m b/x i увеличивается (при этом m b изменяется незначительно). Показатель g степенного хвоста примерно совпадает для различных ионных компонентов КТ и на солнечную активность реагирует гораздо меньше, чем на геомагнитную.
Заметим, что для максвелловских распределений m m = m 0 (Еm = Е0) и коэффициенты x i = 1: при достижении термодинамического равновесия для одного из ионных компонентов такая же температура должна устанавливаться и для остальных компонентов. Однако на экспоненциальном участке спектров обычно m m ¹ m 0 и x i ¹ 1. Следовательно, экспоненциальный участок ионных спектров, так же как и степенной хвост - неравновесный. Проведённый в [99- 103] анализ прямых экспериментальных данных свидетельствует, что весь спектр ионов КТ и ПС - принципиально неравновесный и это справедливо как для возмущённых, так и для спокойных периодов.
В теоретических работах распределения горячей плазмы в геомагнитной ловушке для простоты описываются равновесной (максвелловской) функцией; для анизотропной плазмы постулируются две разные температуры (поперечная и продольная), что также оправдано простотой вычислений и имеет физический смысл: поперечная и продольная теплопроводности замагниченной плазмы различаются очень сильно. Однако для частиц, измеряемых в фиксированном относительно вектора магнитного поля направлении, нередко встречающееся в литературе [32, 66, 73] представление о двух компонентах плазмы, каждая из которых описывается максвелловской функций (“би-максвелловское” распределение) физически абсурдно: максвелловское распределение, по определению, равновесно и описывается единой простой функцией. Такое представление можно использовать только как чисто технический приём: оно очень удобно для вычислений и позволяет достаточно хорошо аппроксимировать реальные интегральные параметры горячей плазмы [104].
Подчеркнём, что выводы [99- 103] - результат перекрёстного анализа огромного массива экспериментальных данных, а не просто наиболее точная аппроксимация ионных спектров. Аппроксимировать же ионные спектры КТ и ближнего ПС в широком энергетическом диапазоне (от нескольких десятков кэВ до нескольких МэВ) можно и единой функций (наиболее близка к полученным в [99- 103] результатам k -функция: j µ E[1 + E/k E0] - k - 1, где k и E0 - параметры), но при этом утрачивается очень важная информация о реальных границах спектральных участков.
Непонимание физической природы энергетических спектров ионов КТ и ближнего ПС и связанный с этим произвол в выборе функций для аппроксимации спектров приводят к ошибочным интерпретациям экспериментальных данных. Так, в [93] ионные спектры ближнего ПС аппроксимировались k -функцией, причём для ионов H+ значения k до и после возмущения брались разными (k = 4.9 - до и k = 1.9 - после начала суббури), а для ионов O+ - одинаковыми (k = 3.9). В результате было получено: параметр E0 увеличивается от ~ 9 до ~ 16 кэВ для спектров ионов H+ и от ~ 9 до ~ 43 кэВ для спектров ионов O+.
Однако из приведённых в [93] спектров видно, что после начала суббури спектры хотя и становятся жёстче (в целом), но различие в форме спектров ионов H
+ и O+ в общем для них диапазоне (~ 30¸ 140 кэВ) невелико. Видно также, что до возмущения параметр k можно определить из этих спектров только с большой погрешностью (прорисовывается только начало степенного хвоста), а после начала суббури спектры ионов H+ и O+ становятся практически степенными с показателем g ~ 1.0¸ 1.3 и оставлять k = 3.9 для спектров ионов O+ нет никаких оснований. Из приведённых в [93] рисунков видно, что при аппроксимации спектров ионов H+ и O+ по единой методике должны получиться близкие значения параметра E0 как до, так и после начала суббури.Заметим, что при достаточно малых энергиях (
E << k E0) ход k -функции задаётся параметром E0 , при больших энергиях - параметром k , а в промежуточной области энергий ход k -функции сильно зависит от конкретных значений как E0 , так и k . Представленные в [93] экспериментальные данные относятся к довольно узкому (особенно для ионов O+) интервалу на границе между экспоненциальным участком и степенным хвостом спектров, причём участки спектров, которые управляются только одним из параметров, одновременно (и достаточно чётко) в приведённых результатах не проявляются (более или менее определённо о таких участках можно говорить только для спектров протонов до возмущения). Из этих данных видно, что однозначно идентифицировать параметры E0 и k по спектрам ионов O+ невозможно даже для спокойных периодов, а после начала суббури это нельзя сделать и для протонов.Таким образом, по данным [93] нельзя говорить о значительном превышении параметров, характеризующих жёсткость суббуревых спектров ионов O
+, над протонными в диапазоне E ~ 40¸ 210 кэВ. Об этом же свидетельствуют и проведённые в [93] результаты статистического анализа 35 суббурь, согласно которым потоки ионов O+ с E ~ 40¸ 210 кэВ в ближнем ПС (r ~ 6¸ 16) возрастали всегда больше, чем потоки протонов тех же энергий, но это различие невелико: при возрастании потоков до порядка величины относительные приращения потоков ионов H + и O+ в среднем различались в 1.37 ± 0.15 раз. Представленные в [93] данные противоречат и предложенной там физической интерпретации (см. раздел 3.3).Проведённый в [99- 103] анализ охватывает практически все основные результаты экспериментальных исследований РП, КТ и ближнего ПС за 40 лет. Результаты этого анализа свидетельствуют, что при m
/x i > 0.5 ± 0.2 кэВ/нТ форма и инвариантные параметры энергетических спектров основных ионных компонентов КТ и ближнего ПС хорошо согласуются друг с другом, т.е. спектры КТ и ближнего ПС связаны простыми аффинными преобразованиями [99- 103]. Более того, инвариантные параметры спектров ионов КТ можно связать со средними параметрами ПС магнитосферного хвоста: показатель степенного хвоста спектров - с долей энергичных частиц в общей плотности энергии частиц и магнитных неоднородностей в ПС, нижнюю границу степенного хвоста спектров - с толщиной и индукцией магнитного поля ПС, среднюю энергию на экспоненциальном участке спектров - с мелкомасштабной структурой (спектром турбулентности) ПС [102, 103]. Эти результаты позволяют сделать заключение, что внешний РП, КТ и ближний ПС связаны гораздо более тесным образом, чем это представлялось ранее, и можно говорить о них как о единой плазменной системе - геокороне горячей плазмы.Подчеркнём, что реальным отображением ПС в геомагнитной ловушке является КТ (частицы с
E > 10¸ 20 кэВ), а не электроны и ионы с E < 10 кэВ. В исследованиях на геосинхронных спутниках ПС идентифицируется иногда по электронам и ионам с E ~ 0.01¸ 10 кэВ, что некорректно: основным источником частиц таких энергий в ловушке является ионосфера (дискретные авроральные структуры), а не ПС. Энергетические, пространственные и питч-угловые распределения частиц с E ~ 0.01¸ 10 кэВ в авроральной области магнитосферы принципиально отличаются от распределений КТ и ПС и очень хорошо коррелируют с AE (см. раздел 3.1.2).В [4] КТ и ПС разделялись резкой пространственной границей. Однако из приведенных там рисунков видно, что эта граница весьма условна и может иметь лишь методический, но не физический смысл. В этой работе КТ идентифицировался по ионам с 80 эВ <
E < 46 кэВ, а ПС - по электронам тех же энергий. В спокойные периоды приведённые в [4] радиальные профили плотности энергии электронов и ионов практически идентичны по форме; такое подобие в основных чертах сохраняется и во время главной фазы бури (поскольку эти данные относятся к частицам с локальным питч-углом a < 45o, наиболее существенные различия в некоторых из этих профилей можно связать с более сильной питч-угловой диффузией и более быстрым высыпанием электронов в конус потерь). Крутая внешняя кромка радиальных профилей плотности энергии плазмы связана с выходом OGO 3 (наклонение 31o) из ПС: на орбитах, проходящих вблизи плоскости эклиптики в ночные часы плотность энергии плазмы ближнего ПС уменьшается с удалением от Земли очень медленно и плавно.На основе полученных в [101- 103] законов скейлинга ионных спектров в [105, 106] разработан новый, инвариантный относительно замены ионных компонентов метод разделения вкладов ионосферного и солнечного источников в КТ и ПС и получены закономерности вариаций ионного состава геокороны во время суббурь и бурь (см. раздел 3.1.3).
Методом “ спектрометра с магнитным парусом” установлены также количественные связи между пространственными, угловыми и спектральными характеристиками потоков ионов КТ в азимутально-асимметричной области ловушки; получены закономерности суточного хода потоков и спектров ионов КТ, хорошо описывающие экспериментальные данные на ГСО [49, 50].
В [107] получены аналитические выражения, связывающие радиальные и энергетические зависимости показателя анизотропии питч-угловых распределений ионов с формой их спектров на внешней границе ловушки. Дано объяснение немонотонности радиального хода, локальных максимумов и минимумов, сильной энергетической зависимости показателя анизотропии. На основе этой теории были установлены основные причины принципиальных расхождений результатов различных экспериментов, все мировые данные согласованы между собой и построена эмпирическая модель квазистационарных ПУР ионов КТ [108].
Полученные в [98- 100] результаты анализа формы спектра протонов КТ позволили на основе развитой в [107] теории, с учётом диссипативных процессов (перезарядки и кулоновского торможения) и реальной топологии магнитного поля, количественно смоделировать все основные закономерности, особенности и нерегулярности в энергетических и радиальных зависимостях анизотропии ПУР протонов КТ [109, 110]. При использовании в моделях КТ протонных спектров другой формы или с другими параметрами получаются не только большие количественные, но и принципиальные качественные расхождения с экспериментами [49, 102, 110].
Динамика ПУР ионов КТ во время бурь моделировалась в [111]. Методами статистической механики эта задача решалась также в более поздних работах [55, 59]. В [55]подтверждён один из основных выводов [107]: ПУР ионов КТ (и РП) в сердцевине и во внешней части ловушки определяются формой граничного спектра ионов в соответствующем энергетическом интервале. Этот вывод представляется в [55] как важнейший новый результат. Однако в [55] рассматривался только участок спектра, отвечающий m
= 0.1¸ 1 кэВ/нТ, для которого использовалась нереалистичная аппроксимация (суперпозиция двух степенных функций).Исходные посылки и основные этапы моделирования ПУР в [111] и в [55, 59] были фактически идентичны и опирались на теорему Лиувилля. Использовалась одна и та же модель электрического поля (из [112]). Однако в отличие от [111], где рассматривалась только главная фаза типичной бури, в [55, 59] рассматривались как главная фаза, так и фаза восстановления конкретных бурь и проводились прямые сравнения расчётов с экспериментальными данными.
Вместе с тем, в [55, 59] рассматривались только простейшие стационарные модели магнитного поля в ловушке, а в [111] использовалась динамическая эмпирическая модель Олсона-Пфитцера. Благодаря этому в [111] получена более полная картина динамики ПУР протонов КТ во время главной фазы бурь. Так, в соответствии с экспериментальными данными [34], в [111] были получены ПУР ионов в форме "бабочки" (с большой отрицательной анизотропией при 36o < a 0 < 142o) для ионов с энергией до ~ 100 кэВ в предполуденном секторе сердцевины ловушки (
L ~ 3.5¸ 4.5). Провал в ПУР при a 0 = 90o формируется в результате адиабатического замедления ионов в процессе их дрейфа через вечерний сектор ловушки во время быстрой локальной депрессии магнитного поля.Развиваемая здесь идея целостности (единства) внешнего РП, КТ и ближнего ПС хорошо вписывается в очень важную концепцию геомагнитосферы [113], согласно которой весь авроральный овал проецируется на область замкнутых силовых линий магнитного поля ближнего ПС и низкоширотная граница овала отвечает нейтральному слою магнитосферного хвоста (то, что мы называем ближним ПС в [113] классифицируется как центральный ПС
).Источником энергии для всех естественных магнитосферных структур и динамических процессов является Солнце. Основная доля солнечной энергии переносится частицами и магнитными полями солнечного ветра.
Во время главной фазы бурь поток энергии из солнечного ветра в геомагнитосферу резко возрастает, усиливая магнитосферно-ионосферную токовую систему (включая КТ и ближний ПС). Увеличение потока солнечной энергии в ионосферу приводит, в свою очередь, к активизации механизмов ускорения и инжекции ионосферной плазмы в магнитосферу. В конечном счёте поступающая в магнитосферу энергия солнечного ветра распределяется между КТ, высыпающимися авроральными частицами, ионосферными токами и одним или несколькими плазмоидами в магнитосферном хвосте.
Некоторая доля солнечной энергии приходит к Земле с электромагнитным излучением, которое является одним из важнейших факторов, определяющих состояние ионосферы и связанной с ней плазмосферы. В свою очередь, эти плазменные оболочки оказывают существенное влияние на состояние и динамику геокороны горячей плазмы (особенно внутренней её области - КТ). Влиянием на геокорону горячей плазмы остальных переносчиков солнечной энергии (СКЛ, нейтронов и нейтрино) можно пренебречь.
Важнейшую роль в преобразованиях магнитосферой энергии солнечного ветра играет ПС. Частицы ПС являются носителями направленного с утра на вечер тока магнитосферного хвоста (тó ковый слой). ПС аккумулирует как солнечную, так и ионосферную горячую плазму и питает ею КТ.
В магнитосферном хвосте все основные динамические процессы (перестройка магнитного поля и ПС) развиваются во время суббурь, а бури отвечают за глобальные возмущения КТ. Одиночные (изолированные) суббури приводят к усилению лишь периферийной (L ~ 5¸ 7) части КТ, которая быстро (в течение ~ 1¸ 2 ч) восстанавливается к стационарному уровню. На главной фазе бурь, которая сопровождается серией суббурь, горячая плазма инжектируется в ловушку гораздо глубже (до L ~ 2¸ 4), причём чем сильнее буря (больше max½ Dst½ ), тем ближе КТ подходит к Земле (в среднем) и тем медленнее (в течение от ~ 1 до ~ 10¸ 15 дней) он восстанавливается.
В общих чертах динамику геокороны горячей плазмы можно описать следующим образом. Процессы ускорения частиц в магнитосферном хвосте, развивающиеся во время суббурь, приводят к разогреву ПС. В результате диполизации силовых линий ближнего ПС и резкого усиления глобального электрического поля эти частицы забрасываются в ловушку, испытывая при этом дополнительное бетатронное ускорение. Некоторая доля горячей плазмы (частицы с энергией от нескольких сотен эВ до 10¸ 20 кэВ) поступает в ловушку непосредственно (минуя ПС) из ионосферы (из низкоширотной области аврорального овала) вдоль магнитных силовых линий.
В ПС движение ионов хаотизировано, а у внешней границы ловушки адиабатичность их движения восстанавливается и они подвергаются дальнейшему ускорению в неоднородных и нестационарных магнитном и электрическом полях.
В результате инжекции горячей плазмы из ПС на главной фазе бури в вечернем секторе ловушки формируется асимметричный КТ и генерируются токи вдоль силовых линий магнитного поля (биркеландовские токи), которые реализуют связи магнитосферы с ионосферой и способствуют быстрой симметризации КТ. Последующее затухание КТ (на фазе восстановления бури) связано с ионизационными потерями (в основном с перезарядкой ионов) и с питч-угловой диффузией частиц в конус потерь в результате циклотронной неустойчивости КТ.
Ускорение ионов до E/Qi ~ 10¸ 20 кэВ в авроральной области осуществляется на высотах h ~ 1¸ 20 тыс. км. Ускорение ионов до более высоких энергий (до нескольких МэВ и более) реализуется в областях вблизи плоскости геомагнитного экватора и обеспечивается хорошо изученным бетатронным механизмом, а также - гораздо более сложными и дискуссионными механизмами, действующими в магнитосферном хвосте и связанными с сильной плазменной турбулентностью, пересоединением магнитных полей (посредством которого плазма перетекает через поверхности, разделяющие области с различной топологией магнитных силовых линий) и стохастичностью движения частиц.
В магнитосферном хвосте ионы могут ускоряться до нескольких МэВ. При этом генерируются ионные пучки, которые распространяются в основном в погранслое (PSBL) ПС - на границе областей разомкнутых и замкнутых силовых линий хвоста. Направленные скорости и энергия частиц в таких пучках хорошо коррелируют с AE. По мере переноса ионов к Земле пучки размываются по энергии и питч-углам (альвеновскими и магнитозвуковыми волнами) и постепенно ассимилируются ПС, внося очень существенный (возможно даже основной) вклад в его состав.
Наиболее важными, ключевыми параметрами, контролирующими состояние и динамику геокороны горячей плазмы являются параметры солнечного ветра (главным образом его скорость Vsw и знак Bz ММП). Эти параметры отвечают как за процессы перестройки структуры магнитного поля во внешних областях магнитосферы и проникновение в магнитосферу солнечной плазмы (управляются Bz), так и за вариации глобального электрического поля (управляется произведением VswBz). Последнее играет очень важную роль в механизмах переноса горячей плазмы в сердцевину магнитосферы.
С различной чувствительностью частиц малых и больших энергий к глобальным электрическим полям связано и различие динамики КТ и РП во время бурь. Основная масса частиц РП обязана своим существованием флуктуациям давления солнечного ветра, а КТ - флуктуациям VswBz . При Bz < 0 достаточно большие скачки VswBz могут вызывать мощную инжекцию частиц из ПС в КТ.
Радиальная диффузия частиц под действием флуктуаций давления солнечного ветра описывается дифференциальным уравнением с линейным оператором переноса. Во внешней части ловушки (L > 4¸ 5) для ионов с m /x i > 0.5 ± 0.2 кэВ/нТ нелинейными диссипативными членами этого уравнения можно пренебречь. Поэтому внешняя область РП, занимающая бó льшую часть ловушки, формируется практически линейным механизмом. Процессы же формирования и динамика КТ принципиально нелинейны: связи между солнечным ветром и КТ включают промежуточные положительные и отрицательные связи через ионосферу (магнитосферно-ионосферные связи). Таким образом, РП можно рассматривать как линейный, а КТ - как нелинейный продукт взаимодействия солнечного ветра с магнитосферой.
РП отличаются от буревого КТ не только по динамике, но и по ионному составу. Если исключить часть ионов с энергией более нескольких МэВ (которые захватываются в геомагнитную ловушку из СКЛ), а также часть ионов внутреннего пояса с энергией более нескольких десятков МэВ (которые имеют альбедное происхождение и связаны с ГКЛ), останется основной массив частиц РП, состав которого сильно отличается от состава ионосферной плазмы и близок к составу солнечного ветра (~ 95¸ 96% всех частиц РП приходится на протоны, ~ 2¸ 5% - на He2+ и ~ 2¸ 5% - на более тяжёлые ионы). Это связано с тем, что ионные компоненты ионосферного происхождения с Mi > 1 (ионы гелия, азота, кислорода и т. д.) вымирают после инжекции их в КТ гораздо быстрее протонов, не успевая набрать необходимую энергию (в результате бетатронного ускорения при радиальной диффузии частиц вглубь ловушки) и перейти в класс РП.
Вместе с тем, в процессах формирования РП и КТ прослеживаются и общие закономерности. Так, для интенсивных бурь с продолжительной (> 3 ч) главной фазой значительный вклад в полную энергию КТ вносит, в дополнение к конвекции, диффузионный перенос частиц из ПС на L ~ 2.5¸ 4.0 под действием флуктуаций глобального электрического поля [39, 55, 59].
Ниже приводится более подробное обсуждение всех этих вопросов.
Ионный состав КТ и ПС контролируется солнечным ветром. Пересоединение магнитного поля солнечного ветра с магнитным полем геомагнитосферы, которое управляется Bz ММП, обеспечивает основные механизмы проникновения солнечной плазмы во внутренние области магнитосферы, а глобальное электрическое поле, которое управляется произведением VswBz , обеспечивает перенос (конвекцию) горячей плазмы от солнечного и ионосферного источников в сердцевину магнитосферы. Благодаря центробежным силам структура конвекции плазмы над полярными шапками и в хвосте магнитосферы зависит от массы ионов (магнитный масс-спектрометр, управляемый солнечным ветром) и, следовательно, вариации параметров солнечного ветра оказывают значительное влияние на ионный состав КТ и ПС.
Так, по данным Горизонта-21 установлено, что на ГСО долговременные (с периодом ~ 1 месяца) вариации потоков ионосферного и солнечного компонентов ионов КТ хорошо коррелируют (с некоторым запаздыванием) со скоростью солнечного ветра [51].
Механизмы разогрева и выноса ионосферной плазмы в магнитосферу (на авроральных широтах) управляются биркеландовскими токами, которые значительно усиливаются в периоды магнитных активизаций [114]. Для соотношения ионосферного и солнечного источников в КТ и ПС очень важна также суббуревая активность магнитосферы.
Роль солнечного источника проявляется в некоторых общих закономерностях ионного и зарядового состава солнечного ветра, КТ и ПС. Так, отношения концентраций [C
6+]/[C5+] и [C]/[O] для ионов с Qi ³ +4 в КТ и ПС коррелируют с этими отношениями в солнечном ветре, где они определяются температурой плазмы [40].На магнитопаузе наблюдается резкое расслоение горячей плазмы плазменной мантии магнитосферы [24, 25]: характеристики плазмы во внешнем слое соответствуют солнечному ветру (точнее, магнитошису), а во внутреннем слое - более горячей магнитосферной плазме, обогащённой ионами O
+ (толщина границы, разделяющей эти слои, составляет всего несколько средних гирорадиусов ионов). Возможно, что указанное расслоение плазмы - артефакт, связанный с волнообразной структурой магнитопаузы (неустойчивость Кельвина-Гельмгольца). Однако если это не так, приходится констатировать, что проникновение частиц солнечного ветра через лобовую область магнитопаузы малоэффективно.Наблюдения показывают также, что магнитопауза является гораздо более жёстким, чем это предсказывалось открытой моделью, препятствием для выхода тяжёлых ионосферных ионов за пределы магнитосферы: во время геомагнитной активности, когда в плазменной мантии магнитосферы наблюдается высокое относительное содержание ионов O
+, магнитопауза является очень резкой границей, отделяющей ионосферные ионы O+ от магнитошиса [24].В экспериментах по программе
AMPTE в солнечный ветер (вблизи границ геомагнитосферы) со спутника IRM дважды инжектировались облака ионов Li+, которые могли регистрироваться высокочувствительными приборами на спутнике CCE внутри магнитосферы. Во время одной из инжекций ММП было направлено на север и, следовательно, магнитосфера была заведомо закрыта для проникновения частиц из солнечного ветра. Однако в другом случае ММП было направлено на юг, но эксперимент также дал отрицательные результаты [82]: во внутренних областях магнитосферы ионы Li+ не регистрировались.Таким образом, магнитопауза практически непрозрачна для частиц солнечного ветра
. Кроме того, даже проникнув в магнитосферу, в ее плазменную мантию, только незначительная доля солнечных ионов просачивается затем в ПС, что подтверждается как экспериментальными данными, так и модельными расчётами [115]. И даже если бы в ПС беспрепятственно попадали все ионы магнитошиса, они не обеспечили бы наблюдаемых во время магнитных возмущений концентраций ионов с E/Qi < 17 кэВ в КТ в дневной части магнитосферы [24].С другой стороны, в экспериментальных исследованиях установлено, что изнутри проницаемость магнитопаузы для частиц горячей плазмы гораздо выше, чем снаружи. В периоды геомагнитной активности спектры ионов в магнитошисе (вблизи магнитопаузы) становятся жёстче, причём в вечерних областях магнитошиса они варьируют сильнее, чем в утренних [116], что свидетельствует об активной роли магнитосферы в модуляции энергетических спектров горячей плазмы магнитошиса.
Высвобождение горячей плазмы из магнитосферы обеспечивается пересоединением магнитосферного и межпланетного магнитных полей. Однако такое пересоединение имеет кратковременный импульсный характер и не объясняет всей совокупности экспериментальных данных. По-видимому, ионы с
E < 10 кэВ (накопленные в пограничном слое) высвобождаются из магнитосферы в результате "раскрытия" магнитосферных силовых трубок в магнитошис при пересоединении магнитных полей, а более энергичные ионы в ходе дрейфа могут пересекать магнитопаузу и покидать магнитосферу и в отсутствие пересоединения полей (в подсолнечной области магнитосферы у её границы конвекция горячей плазмы направлена к Солнцу).Большое различие в проницаемости магнитопаузы для частиц горячей плазмы снаружи и изнутри магнитосферы связано со вторым началом термодинамики: при выходе из магнитосферы плазма попадает в область более хаотичного движения частиц магнитошиса (где магнитное поле слабее и сильно турбулизовано) и энтропия плазмы увеличивается, а при обратном переходе энтропия плазмы должна уменьшаться, что невозможно (это не относится к частицам высоких энергий - СКЛ и ГКЛ). По этой же причине ограничено и проникновение солнечной плазмы в магнитосферу через полярные каспы. И хотя в каспах наблюдались значительные всплески потоков солнечных ионов с
E/Qi = 1¸ 200 кэВ и более [117], только ничтожная доля этих ионов может проникать в сердцевину магнитосферы.По современным представлениям, бó льшая часть содержащихся в геомагнитосфере солнечных частиц поставляется в неё через магнитосферный хвост, куда солнечная плазма проникает в основном в результате пересоединения межпланетного и магнитосферного магнитных полей и конвекции плазмы поперёк хвоста вблизи плоскости эклиптики [74, 76]. На замкнутые силовые линии частицы солнечной плазмы захватываются в основном в районе дальней нейтральной линии (
r > 45) токового слоя хвоста [92, 97].Проникновение солнечной плазмы в геомагнитосферу через ПС чётко прослеживается по ионному составу горячей плазмы. Так, по экспериментальным данным, полученным в ночной области ближнего ПС (на
r ~ 7¸ 9), отношение усредненных по Kp концентраций [C6+ + C5+ + C4+]/[O7+ + O6+] = 0.65 ± 0.02 [40], что хорошо согласуется с усредненным за 3 месяца значением этой величины (» 0.66 ± 0.10) в дальнем (r ~ 200) хвосте геомагнитосферы [94].В результате статистического анализа экспериментальных данных установлено [79], что время переноса солнечной плазма в ближний ПС (на
r ~ 20) составляет ~ 1¸ 2 ч, а на ГСО - от ~ 4 ч (в полуночный сектор) до ~ 15 ч (в полуденный сектор).До недавнего времени полагалось, что перенос плазмы от дальней нейтральной линии во внутренние области геомагнитосферы реализуется конвекцией. Однако современные эксперименты свидетельствуют, что в сердцевине ПС конвекция слабая и хотя средние скорости частиц на
r < 45 направлены к Земле, но они очень малы и не соответствуют экспериментальным оценкам времён переноса солнечной плазмы [79], а на r > 60 потоки частиц в ПС почти всегда направлены от Земли [95]. В современных моделях [79] перенос плазмы к Земле от дальней нейтральной линии реализуется не в сердцевине ПС, а в погранслое (PSBL) ПС; при этом учитывается конвекция и турбулентная диффузия частиц поперек магнитных силовых линий из PSBL в сердцевину ПС. Такому переносу солнечной плазмы не препятствует ни пересоединение магнитных силовых линий в хвосте магнитосферы, ни направленные от Земли потоки плазмы в сердцевине ПС. Ионный состав PSBL в среднем примерно такой же как в сердцевине ПС.Ионосферная плазма истекает в магнитосферу на всех широтах. Всю ионосферу можно разделить на три основные области, которые сопрягаются (вдоль магнитных силовых линий) с различными структурами холодной и горячей плазмы в магнитосфере: ионосфера на низких и средних широтах связана с плазмосферой, над полярными шапками - с долями магнитосферного хвоста, на промежуточных широтах и в авроральной области - с КТ и ближним (центральным) ПС. В первых двух областях температура истекающей из ионосферы плазмы (полярного ветра) в спокойных условиях не превышает нескольких эВ [118]. Поэтому спокойный полярный ветер и плазмосфера состоят в основном из протонов (и электронов): в отличие от электронов и протонов, ионы O
+ не преодолевают более высокий для них гравитационный барьер (~ 10.5 эВ).Ускорение ионосферных ионов до энергии
E ~ 10¸ 20 кэВ, которая отвечает средней энергии ионов в ближнем ПС и нижней границе спектров КТ, реализуется на широтах аврорального овала. Для описания ионосферного источника горячей магнитосферной плазмы используются два типа моделей: авроральные и касповые (полярные каспы проецируются вдоль магнитных силовых линий на дневную часть аврорального овала).В авроральных моделях рассматриваются две стадии ускорения ионосферных ионов: на первой стадии ионы ускоряются плазменной турбулентностью поперёк магнитного поля до нескольких десятков или сотен эВ (на
h < 1 тыс. км), а на второй стадии - двойными слоями с продольными электростатическими полями (солитонами) [119] или низкочастотными флуктуациями поперечного электрического поля [120] до нескольких кэВ или нескольких десятков кэВ (на h ~ 7¸ 10 тыс. км). Двухступенчатому ускорению отвечают характерные питч-угловые распределения ионов с энергией до нескольких десятков кэВ (“бимодальные коники”), часто наблюдаемые в авроральной области [119, 120].Ускорение ионосферных ионов, фонтанирующих из полярных каспов, также проходит две стадии: под действием плазменной турбулентности в каспах (первая стадия) и под действием конвективных электрических полей в ходе переноса ионов над полярными шапками из каспов во внешние области ночной магнитосферы (вторая стадия). Измерения спектров частиц и волн подтверждают теорию ускорения ионов O
+ циклотронными волнами в районе полярных каспов [121].В [51] был предложен и апробирован на данных Горизонта-21 метод разделения вкладов аврорального и каспового источников ионов КТ по величине запаздывания между долговременными (с периодом ~ 1 месяца) вариациями потоков различных ионных компонентов КТ на ГСО и вариациями
Kp- индекса.Ионы могут ускоряться также электростатическими или электромагнитными циклотронными волнами [122], генерируемыми протонами КТ (стохастические механизмы). Поскольку гирочастота W
i µ Qi/Mi и спектральная плотность волн быстро уменьшается с ростом частоты, эффективность ускорения ионов O+ такими волнами выше, чем ионов H+. Это проявляется во время суббурь: в пучках ионосферных ионов на авроральных широтах средняя энергия O+ в ~ 2 раза больше средней энергии H+ [24, 67].Ионный состав частиц, вылетающих из верхней ионосферы, формируется в основном на первом этапе ускорения и в значительной степени определяется не только составом верхней ионосферы, но и уровнем плазменной турбулентности, продольными электрическими полями, процессами перезарядки [123], а также потоками тепла, переносимого из магнитосферы в ионосферу электронами и высыпающимися в атмосферу энергичными ионами. В различных механизмах истечения ионосферной плазмы её ионный состав различается.
Необходимое условие вытягивания ионов из ионосферы - превышение некоторого критического значения для поперечной скорости ионов - способствует формированию ионных спектров с x
i = Mi [124]. Однако по мере неадиабатического ускорения ионов электрическими полями параметр x i должен постепенно трансформироваться от Mi к Qi .Временные и пространственные зависимости элементного и зарядового состава горячей плазмы в геомагнитосфере могут объясняться тем, что различные механизмы ускорения и выноса ионосферных частиц в магнитосферу по-разному зависят от геомагнитной (а также солнечной) активности и сферы их влияния в магнитосфере различны. Вследствие особенностей траекторий частиц в магнитосфере различные области геокороны горячей плазмы заполняются ионами из различных областей ионосферы: на
r > 10¸ 20 основной вклад дают полярные каспы, а на меньших расстояниях - ночная часть аврорального овала [118]. В отличие от O+, лёгкие ионы (H+) могут заполнять более удаленные области магнитосферы; поэтому с увеличением r следует ожидать уменьшения отношения [O+]/[H+] в ПС, что согласуется с экспериментальными данными [26, 71].По данным, полученным над авроральным овалом в разные периоды и на разных высотах, средние соотношения потоков различных ионных компонентов близких энергий (~
0.1¸ 20 кэВ) сильно различаются. Так, по данным S3-3, на h ~ 1 RE, средние потоки ионов H+ в интервале 0.5¸ 16 кэВ в ~ 6 раз превышали потоки ионов O+, хотя наблюдались значительные вариации этого соотношения [125], а по данным Прогноз-7, на h ~ 3¸ 5 RE, в потоках ионосферных ионов с E = 0.2¸ 17 кэВ доминировали ионы O+ [24]. Такое различие может свидетельствовать, что ионы O+ наиболее эффективно ускоряются на h > 1 RE или/и пучки ионов H+ на h > 1 RE сильнее размываются питч-угловой диффузией. Поскольку эксперимент S3-3 проводился в минимуме, а Прогноз-7 - вблизи максимума солнечной активности, указанное расхождение может быть связано также с солнечно-циклическими вариациями.С ростом солнечной активности увеличивается интенсивность ультрафиолетового излучения, что приводит к увеличению скорости ионизации верхней атмосферы и разогреву ионосферы. Это облегчает выход O
+ (и других ионосферных ионов с Mi >> 1) в магнитосферу. По данным S3-3 и ISEE-1 показано [126], что с ростом солнечной активности увеличивается и эффективность ускорения ионов на h > 1 RE. В результате компьютерного моделирования показано, что при переходе от минимума к максимуму солнечной активности потоки энергичных ионов O+ на авроральных широтах должны увеличиваться на порядок величины [127]. Судя по данным AMPTE/CCE, связь между концентрациями энергичных ионов с Mi >> 1 в геомагнитосфере и интенсивностью ультрафиолетового излучения Солнца нелинейна [40], причём существует, по-видимому, некоторый порог по интенсивности излучения, выше которого данная зависимость резко ослабляется.Многие наблюдения свидетельствуют, что ионосферный источник горячей плазмы активизируется на главной фазе бурь. Так, в начале главной фазы бури 4 сентября 1984 на
L = 6.5¸ 7.0 были зарегистрированы повышенные потоки типично ионосферных молекулярных ионов [NO]+ и O2+ с энергией до нескольких сотен кэВ, а на фазе восстановления бури (через ~ 1.5 дня после ее начала) они практически полностью исчезли [31]. В спокойные периоды в потоках ионосферных ионов доминируют протоны, а во время суббурь резко увеличивается вклад ионов O+: суммарный поток ионов O+ с E = 0.5¸ 16 кэВ в авроральной зоне возрастает более чем на порядок величины, а поток ионов H+ увеличивается всего в ~ 3 раза [128].Потоки выносимых из ионосферы ионов O
+ резко усиливаются на взрывной фазе суббурь: на подготовительной фазе и на фазе роста суббурь плотность их энергии возрастает с ростом AU линейно, а на взрывной фазе - экспоненциально [85]. Резкое усиление электрического поля конвекции в конце фазы роста суббурь приводит к усилению (посредством биркеландовских токов) аврорального электроджета и к резкой активизации авроральных механизмов ускорения, что проявляется в хорошей корреляции плотности энергии ионов O+ в ближнем ПС с индексом AU [52, 85]. Энергичные ионы О+ реализуют в этих процессах положительную обратную связь между ионосферой и магнитосферой, способствуя развитию взрывной фазы суббури [37, 52, 85]. В продолжительные периоды повышенной авроральной активности плотность энергии ионов O+ в ближнем ПС постепенно увеличивается [45, 52, 85].Горячая ионосферная плазма может инжектироваться в ПС и накапливаться там, смешиваясь с солнечной плазмой, и постепенно конвектировать в ловушку. Однако, по наблюдениям на спутниках, во время магнитных активизаций ионы с
E/Qi < 20 кэВ заполняют ловушку (3 < L < 8) гораздо быстрее, причём потоки ионов O+ возрастают на всех LT и днём отношение потоков ионов O+/H+ таких энергий больше, чем ночью [24]. На основании этих фактов можно говорить о прямой инжекции ионосферных ионов с E/Qi < 20 кэВ в ловушку (вдоль силовых линий магнитного поля).Согласно данным ISIS-2 [129] и DE-1 [130], а также оценкам скорости заполнения плазмосферы по данным о вистлерах, потоки полярного ветра на ионосферных высотах составляют ~ 3¸ 5× 108 cм- 2c- 1. Этим значениям отвечают суммарный (в интервале широт 51¸ 90о) поток плазмы из ионосферу в магнитосферу ~ 3¸ 5× 1026 c- 1 [118], что всего в несколько раз меньше потока солнечного ветра на геомагнитосферу (~ 0.7¸ 1.4× 1027 c- 1). Учитывая, что в геомагнитосферу проникает только небольшая (несколько %) доля потока солнечного ветра, следует признать, что ионосферный источник вносит основной вклад в общую концентрацию плазмы в геомагнитосфере и, несомненно, доминирует в холодном компоненте плазмы.
Однако суммарный поток горячей плазмы, направляемый в магнитосферу от ионосферного источника в авроральной области (E/Qi ~ 0.5¸ 16 кэВ) и поступающий в КТ и ПС, по экспериментальным данным составляет (1¸ 3) 1025 c- 1 для H+ и (0.27¸ 4.2) 1025 c- 1 для O+ [128]. Из каспов фонтанирует ~ 1025 c- 1 ионов H+ и O+ [131]. Эти потоки соизмеримы с потоками горячей плазмы, поступающей в геомагнитосферу из солнечного ветра (модель [118] сильно преувеличивает роль ионосферного источника в формировании ионного состава КТ и ПС).
По результатам измерений ионного состава КТ в диапазоне E/Qi ~ 0.1¸ 17 кэВ установлено, что в различных бурях могут доминировать как солнечный, так и ионосферный источник частиц, а в некоторых бурях активно функционируют оба источника [20, 25, 26]. Это положение чётко прослеживается также в зарядовых спектрах ионов углерода и кислорода с Qi от + 1 до Zi и E/Qi » 1¸ 300 кэВ ближнего (r ~ 8¸ 9) ПС [32].
Экспериментальные данные свидетельствуют, что в спокойные периоды полное число ионов КТ и ближнего ПС складывается в основном из протонов; во время геомагнитных возмущений протоны обычно также доминируют в составе КТ и ПС (кратковременное доминирование ионов O+ наблюдается только в конце главной фазы и в начале фазы восстановления гигантских бурь). Поэтому очень важно правильно определить относительные вклады ионосферного и солнечного источников именно в протонный компонент.
Решение системы уравнений баланса парциальных концентраций различный ионных компонентов, учитывающей законы скейлинга ионных спектров (см. раздел 2) и зависимость эффективности ионосферного источника от заряда и массы ионов, позволяет получить по данным GEOS-1, GEOS-2, ISEE-1, SCATHA, AMPTE/CCE и AMPTE/IRM хорошо согласующиеся друг с другом оценки долей ионосферных и солнечных протонов в КТ и ПС [105, 106]. Показано, что в спокойном ближнем ПС (r = 10¸ 23) протонов ионосферного и солнечного происхождения примерно поровну (50 ± 5%), причём для диапазонов Е/Qi = 0.1¸ 16 и 25¸ 230 кэВ получены очень близкие оценки. Во время суббурь ближний ПС обогащается ионосферными протонами (их доля увеличивается до 75 ± 5%); по отношению к протонам доля O+ увеличивается в ~ 2 раза для Е/Qi = 25¸ 230 кэВ и более чем на порядок величины для Е/Qi = 0.1¸ 16 кэВ, а доля He+ почти не меняется. Таким образом, возмущённый ближний ПС состоит в основном из ионосферной плазмы.
По результатам проведённых в [105, 106] вычислений, в спокойном КТ большинство протонов (> 70%) имеют ионосферное происхождение (на L = 5¸ 7 средняя доля ионосферных протонов составляет 83¸ 85%) и с уменьшением L доля солнечных протонов монотонно понижается. Во время бурь КТ обогащается солнечными частицами и доля солнечных протонов в КТ приближается к соответствующей величине в спокойном ПС. Вместе с тем, во время бурь и суббурь увеличиваются поставки в КТ ионосферных ионов (преимущественно O+) и верхний порог ускорения ионосферных ионов вблизи их источника увеличивается от ~ 1 до ~ 20 кэВ. Как в спокойных условиях, так и во время геомагнитных возмущений влияние ионосферного источника увеличивается с приближением точки наблюдения к авроральной зоне.
Так, во время главной фазы гигантской бури в феврале 1986 более 70% протонов с E ~ 1¸ 315 кэВ поступало на L = 3¸ 7 из гелиосферы; однако уже к началу медленной фазы восстановления состав КТ восстанавливался, причём доля ионосферных протонов по сравнению с солнечными была даже выше, чем во время менее мощных бурь [106].
От минимума к максимуму солнечной активности КТ обогащается тяжёлыми ионосферными ионами, особенно ионами O+, но при этом доля ионосферных протонов в полном числе протонов КТ уменьшается; ПС гораздо слабее реагирует на солнечный цикл [106].
Результаты [105, 106] хорошо вписываются в современную картину энергетического баланса солнечно-земных и магнитосферно-ионосферных связей и могут служить одним из наиболее сильных аргументов в пользу моделей суббури с пересоединением магнитных полей в хвосте магнитосферы (эти результаты относятся к суббурям, развивавшимся во время бурь).
Из результатов проведённого в [105, 106] анализа следует, что в промежутках между суббурями ионосферные и солнечные протоны обобществляются в ПС, доускоряются и перераспределяются по энергии в широком энергетическом диапазоне (Е/Qi ~ 0.1¸ 100 кэВ); при этом спектры протонов различного происхождения переформируются и протоны "забывают" о своём происхождении (эта информация сохраняется только в парциальных концентрациях более тяжелых ионов). Отсюда следует, в частности, что метод разделения протонов КТ и ПС на ионосферные и солнечные по форме их энергетических спектров некорректен.
В некоторых работах по экспериментальным данным, полученным в узком энергетическом диапазоне или/и в ограниченном интервале L, делались общие выводы о доминировании того или иного источника ионов КТ. Рассмотрим несколько таких примеров.
На спаде геомагнитной активности и в спокойные периоды отношение потоков O+/H+ с E/Qi = 0.9¸ 16 кэВ в области ГСО постепенно уменьшается, откуда делалось заключение, что солнечный источник доминирует в КТ [20]. Однако этот вывод нуждается в коррекции с учётом изменений в КТ отношения потоков He2+/H+: поскольку в указанные периоды уменьшается не только O+/H+, но и He2+/H+, увеличивается роль ионосферного (а не солнечного) источника, причём в составе ионосферных ионов преобладают протоны.
В диапазоне Е/Qi < 17 кэВ ионы O+ вносят основной вклад в плотность энергии горячей плазмы на L ~ 4 в спокойные периоды и на L ~ 4¸ 8 - во время магнитных активизаций [23, 24]. Из этих фактов делается заключение [23, 24], что усиление КТ обеспечивается в основном ионосферным источником. Однако при этом не учитывается, что максимум дифференциальной плотности энергии КТ приходится на Е/Qi ~ 30¸ 400 кэВ в спокойные периоды и на ~ 30¸ 80 кэВ (в зависимости от L) - во время магнитных активизаций, а вклад ионов с Е/Qi < 17 кэВ в полную энергию КТ не превышает ~ 10% [12, 32] и, следовательно, выводы, полученные для ионов с Е/Qi < 17 кэВ, нельзя экстраполировать на весь КТ. Во время бурь основными (~ 80%) носителями полной энергии КТ являются ионы с Е/Qi ~ 20¸ 250 кэВ [12, 32]. Эти ионы приходят в ловушку из утренних областей ближнего (r > 7) ПС [25], где они имеют энергию Е/Qi < 17 кэВ и в основном солнечное происхождение: средние значения отношения концентраций [O+]/[H+] здесь примерно на порядок величины ниже, а [He2+]/[H+] - несколько выше, чем в других областях ПС [25].
Во время главной фазы типичных бурь [O+]/[H+] и [He+]/[H+] уменьшаются в КТ (при r < 6) и увеличиваются в ПС [25], причём в промежуточной области (r ~ 6¸ 8) увеличивается как [He2+]/[H+], так и [O+]/[H+] [20]. По-видимому, эти результаты нельзя интерпретировать только как следствие изменений относительной роли ионосферного и солнечного источников горячей плазмы; они указывают на то, что для различных ионных компонентов интенсивность ионосферного источника меняется во время геомагнитной активности по-разному [105, 106].
Некоторую, хотя и не очень значительную, роль в формировании ионного состава КТ и ПС может играть плазмосфера: во время бурь оторвавшиеся от неё облака холодной плазмы, в составе которых на втором месте (после протонов) стоят ионы Hе+, в дневные часы выносятся конвекцией к магнитопаузе; в токовом слое магнитопаузы ионы ускоряются до E > 1 кэВ и часть из них возвращается в ловушку через ПС. В пользу такого механизма свидетельствуют следующие факты: вблизи лобовой точки магнитопаузы потоки энергичных ионов Hе+ часто доминируют над потоками ионов O+, а на флангах магнитосферы соотношение их потоков обратное [132].
Расчётная эффективность ионосферного источника для He+ с E > 10 кэВ на L = 3¸ 5 выше, чем для протонов [105, 106], что может указывать на существенное влияние плазмосферы на ионный состав КТ в этой области. Преимущественное ускорение плазмосферных ионов He+ до энергий КТ может происходить в районе плазмопаузы в результате резонанса с циклотронными волнами.
В ближнем (r ~ 7¸ 18) ПС, по усредненным для спокойных и возмущенных периодов данным, спектры ионов H+ и He2+ в диапазоне Е/Qi ~ 10¸ 160 кэВ подобны с x i » Qi и мягче спектров ионов He+ и O+, а радиальный градиент потоков для первой пары ионов меньше, чем для второй [84]. Поэтому можно полагать, что пространственно-энергетические распределения ионов ближнего ПС формируются неадиабатическими процессами, причём с уменьшением r роль ионосферного источника возрастает.
Одним из наиболее разработанных механизмов ускорения и формирования пространственно-энергетических распределений частиц ПС является модель токового слоя магнитосферного хвоста. Согласно этой модели ионы захватываются токовым слоем хвоста на утреннем фланге магнитосферы, дрейфуют поперёк хвоста на вечернюю сторону и уходят из токового слоя (вдоль магнитных силовых линий) на вечернем фланге магнитосферы. При этом ионы ускоряются под действием направленного с утра на вечер электрического поля. Поскольку в токовом слое ПС электрическое поле примерно такое же как в ПС в целом, а Bz » 0, формально скорость электрического дрейфа частиц в этом слое стремится к бесконечности. Реально же это сопровождается нарушением адиабатических инвариантов движения частиц.
При нарушении m и/или I движение частиц в ПС хаотизируется и реализуется стохастическое рассеяние и ускорение ионов [133- 138]. В квазистационарном хвосте адиабатичность движения частиц нарушается при k = (Rc/r i)1/2 < 3, где Rc - минимальный радиус кривизны магнитной силовой линии и r i максимальный гирорадиус частицы [138], т.е. параметр k относится к вершине силовой линии. Компьютерное моделирование при 1 < k < 3 показывает, что m систематически увеличивается для ионов с a 0 < 30о и слабо меняется для ионов с a 0 ~ 90 ± 60o [138]. Поскольку для ионов с одинаковыми скоростями r i µ Mi /Qi , по сравнению с протонами внутренняя граница области стохастического рассеяния и ускорения ионосферных ионов группы CNO располагается ближе к Земле.
Однако в квазистационарных моделях магнитосферного хвоста ускорение ионов сравнительно невелико, составляя несколько десятков процентов от их начальной энергии без учёта [139] и немного больше - с учётом хаотизации движения ионов [135, 138]. По сравнению с пространственным, нарушение временнó го критерия адиабатичности приводит к гораздо более эффективному стохастическому ускорению (и питч-угловой диффузии) ионов. В динамических моделях токового слоя во время взрывной фазы суббури энергия ионов может увеличиваться в ~ 103 раз на r ~ 10¸ 15 [137] и в ~ 103¸ 105 раз - в районе нейтральной линии [136].
Временнó
й критерий адиабатичности движения (сохранения m
) ионов реализуется при ![]() , где
, где ![]() -
гиропериод частиц. Результаты компьютерного моделирования свидетельствуют, что эффективность стохастического ускорения ионов тем выше, чем больше величина c
и m
нарушается уже при c
> 0.05 [137]. Эффективность такого ускорения сильно зависит от питч-угла частицы. Ионы с a
0 »
90o ускоряются только в самом начале коллапса магнитного поля и быстро убегают из области ускорения, немного смещаясь при этом к Земле. Незначительно и ускорение ионов с малыми a
0 , поскольку в приэкваториальной области, где коллапс наиболее эффективен, они проводят малую часть периода осцилляций. Наиболее эффективно ускоряются ионы, которые в начале коллапса находились на промежуточных (l
*
~
12o) широтах [137]. Поскольку для ионосферных ионов группы CNO Mi /Qi >> 1, они могут ускоряться более эффективно, чем протоны.
-
гиропериод частиц. Результаты компьютерного моделирования свидетельствуют, что эффективность стохастического ускорения ионов тем выше, чем больше величина c
и m
нарушается уже при c
> 0.05 [137]. Эффективность такого ускорения сильно зависит от питч-угла частицы. Ионы с a
0 »
90o ускоряются только в самом начале коллапса магнитного поля и быстро убегают из области ускорения, немного смещаясь при этом к Земле. Незначительно и ускорение ионов с малыми a
0 , поскольку в приэкваториальной области, где коллапс наиболее эффективен, они проводят малую часть периода осцилляций. Наиболее эффективно ускоряются ионы, которые в начале коллапса находились на промежуточных (l
*
~
12o) широтах [137]. Поскольку для ионосферных ионов группы CNO Mi /Qi >> 1, они могут ускоряться более эффективно, чем протоны.
Благодаря многочисленным экспериментальным наблюдениям ионных пучков (с энергией от нескольких кэВ до нескольких МэВ) в хвосте магнитосферы [69, 70, 72] теории, основанные на модели токового слоя и пересоединении магнитных полей, в последние 10- 15 лет получили большое развитие. Согласно таким теориям, критический момент динамики токового слоя в ходе его утоньшения на фазе роста суббурь наступает при приближении радиуса кривизны силовых линий магнитного поля к среднему гирорадиусу ионов в этом слое. Дальнейшая эволюция токового слоя определяется стохастизацией траекторий частиц, которая отвечает, по-видимому, за начало быстрого пересоединения магнитных полей хвоста и переход от подготовительной к взрывной фазе суббури; эта стадия имеет существенно нелинейный характер и описывается теорией катастроф [133- 135]. Однако конкретные сценарии пересоединения полей и динамики хвоста в настоящее время являются предметом дискуссий.
В связи с этим заметим, что измерения на одном спутнике не позволяют делать однозначных выводов о топологии магнитного поля в достаточно удалённых от Земли областях магнитосферного хвоста (поскольку силовые линии хвоста могут быть сильно перекручены, критерии, связанные со знаком Bz в токовом слое, не работают). Так, по данным ISEE-3 было сделано заключение, что бó льшая часть магнитных силовых линий долей хвоста разомкнута [77], а в [81] на основании тех же экспериментальных данных утверждается, что квазистационарной нейтральной линии в ПС нет по крайней мере до r ~ 220 и значительная часть силовых линий полярных шапок и долей геомагнитного хвоста замкнута.
Кратковременные высокоскоростные (> 400 км/с) потоки плазмы иногда наблюдаются даже в нейтральном слое [87, 88], причём при AE < 300 нТ вероятность их появления в сердцевине ПС ~ 1%, а при AE > 600 нТ она достигает 6%, что даже больше, чем в PSBL [87]. Поэтому можно полагать, что не только область нейтральной линии токового слоя, но и значительная часть (если не весь) ПС относится к наиболее активной (с точки зрения ускорения ионов) области геомагнитного хвоста.
Для описания физических процессов, развивающихся при перестройке конфигурации магнитосферного хвоста, разработана теория разрывной (tearing) неустойчивости токового слоя. Согласно этой теории, при перестройке поля хвоста в токовом слое образуются локальные магнитные структуры с характерными размерами ~ нескольких тыс. км (магнитные острова), на границах которых магнитное натяжение очень мало. Рождение магнитных островов сопровождается сильным ускорением частиц на их границах, где структура поля такая же, как в области нейтральной линии токового слоя.
При некоторых условиях такая неустойчивость может реализоваться в две стадии: начальной линейной и последующей нелинейной (взрывной). На линейной стадии формируются спектры частиц с высокоэнергичным экспоненциальным хвостом, а на взрывной стадии этот хвост становится степенным. Последовательное развитие tearing-неустойчивости от линейной к взрывной фазе формирует спектры с экспоненциальным участком, переходящим в степенной хвост [140].
Теория tearing-неустойчивости токового слоя объясняет многие особенности пространственно-энергетической структуры и динамики ПС (в частности - большую протяжённость области ускорения частиц в магнитосферном хвосте). Однако современные варианты этой теории в целом не согласуются со многими экспериментальными результатами [78, 102, 141].
Важнейшим параметром в механизмах ускорения частиц в магнитосферном хвосте является величина Bz в нейтральном слое: адиабатичность движения частиц в ближнем ПС нарушается при Bz < 1 нТ [139]. Однако в результате статистического анализа установлено, что на r ~ 10¸ 22 в нейтральном слое вблизи полуночного меридиана <Bz> » 4.65 нТ (5 < Bz < 8 нТ) в спокойные периоды и <Bz> » 8.13 нТ - в периоды продолжительной суббуревой активности [75]. Для ближнего ПС (r ~ 10¸ 20) эти результаты исключают возможность существования крупномасштабных (с размерами > RE) областей нейтрального слоя с Bz < 1 нТ в течение достаточно продолжительных интервалов. Такой вывод ставит под сомнение возможность пересоединения магнитных полей и высокую эффективность гипотетических неадиабатических процессов ускорения ионов в ближнем ПС.
Кроме того, реальная толщина токового слоя гораздо меньше принятой во многих теоретических моделях величины (~ 2 RE) и составляет иногда всего несколько сотен км [75]. В связи с этим заметим, что чем тоньше токовый слой, тем хуже согласуются друг с другом расчётные и экспериментальные спектры ионов ПС [140].
По мере приближения точки наблюдения к Земле концентрация и температура ПС увеличиваются, но магнитное поле возрастает при этом быстрее [79]. Следовательно, на r > 12 (где b > 1) ближний ПС, особенно его сердцевина, турбулизован, что проявляется и в питч-угловых распределениях ионов [88]: в спокойные периоды и для медленных (< 100 км/с) потоков плазмы во время суббурь распределения ионов ПС изотропны. Плазменная турбулентность приводит также к ускорению частиц и выравниванию параметров плазмы в различных областях ПС.
Можно надеяться, что в настоящее время основные принципиальные механизмы ускорения и переноса частиц в магнитосферном хвосте установлены. Однако создать универсальную теорию магнитосферного хвоста пока не удаётся: одни особенности распределений частиц в ПС и закономерности их динамики во время суббурь согласуются с моделями пересоединения магнитных полей и разрыва токового слоя, другие - с турбулентными моделями. Кроме того, следует иметь в виду, что все рассмотренные механизмы известны нам только в общих чертах. Основанные на них количественные модели состава, структуры и динамики ПС содержат свободные параметры, определение и уточнение которых требует дальнейшей работы.
Модели магнитосферного хвоста и механизмы ускорения частиц в этой области магнитосферы тесно связаны с проблемой суббурь. Поэтому теория магнитосферного хвоста получит завершённую форму по-видимому только вместе с теорией суббурь, которая в настоящее время сталкивается с рядом сложных проблем (рассмотрение их выходит за рамки данного обзора).
Основной механизм ускорения частиц в окрестности экваториальной плоскости на периферии геомагнитной ловушки и в примыкающих к ней областях ближнего ПС - бетатронное ускорение на взрывной фазе суббурь, когда магнитное поле быстро (в течение ~ 1¸ 2 мин) восстанавливается (диполизуется) и силовые линии, вытянутые в хвост на фазе роста суббурь, втягиваются в ловушку. При этом в приэкваториальной околополуночной области авроральной магнитосферы генерируются вихревые электрические поля с напряжённостью до ~ 15¸ 30 мВ/м, которые наблюдались на спутниках [57] и могут ускорять ионы до энергий в несколько сотен кэВ [83, 93]. Так, по наблюдениям на Geotail, с началом диполизации магнитного поля совпадали (в пределах < 1 мин) внезапные увеличения потоков ионов H+ и O+ с E ~ 100 кэВ в ближнем ПС [93]. В отличие от суббурь, во время бурь влияние вихревых электрических полей на динамику частиц КТ невелико [142].
Для интерпретации суббуревых всплесков потоков частиц на периферии ловушки и в ближнем ПС часто привлекался очень популярный адиабатический механизм ускорения частиц в результате медленного вытягивания и последующего быстрого (по сравнению со временем дрейфа частиц через эту область) сокращения магнитных трубок ("рогатка Тверского"), предложенный в [143]. Из наблюдений на геосинхронных и других спутниках хорошо известно, что более или менее значительные быстрые изменения конфигурации магнитных трубок в районе полуночного сектора (суббури и микросуббури) обеспечивают практически непрерывную подкачку плазмы из ПС в КТ; в результате такой подкачки поддерживается азимутальная асимметрия КТ в авроральной области, необходимая для генерации наблюдаемых биркеландовских токов зоны I. Квазипериодические изменения конфигурации магнитных трубок ночной авроральной области обеспечивают перемешивание и непрерывный обмен плазмой между КТ и ПС; это один из важнейших механизмов, связывающих КТ и ближний ПС в единую систему - геокорону горячей плазмы (к важнейшим механизмам такого рода относятся также конвекция и радиальная диффузия горячей плазмы).
Однако эффективное ускорение частиц таким механизмом может реализоваться только при двух дополнительных условиях [143]: а) солнечная плазма свободно втекает в ПС через утренний его фланг, переносится конвекцией поперёк ПС и выходит из него на вечернем фланге ПС; б) силовые трубки вытягиваются в хвост магнитосферы в результате возрастания давления плазмы в солнечном ветре и в ПС, а при последующем уменьшении давления солнечного ветра они быстро сокращаются и втягивают плазму в ловушку, что сопровождается бетатронным ускорением частиц. Таким образом, рассмотренная в [143] модель предполагает, что "рогатка" срабатывает под действием вариаций давления плазмы в солнечном ветре и в ходе вытягивания магнитных трубок (силовые линии остаются замкнутыми) они непрерывно обновляются свежей солнечной плазмой, причём сокращаются они гораздо быстрее, чем растягиваются.
Но по современным представлениям вытягивание силовых линий в хвост геомагнитосферы связано не с увеличением давления плазмы в ПС, а с усилением токового слоя хвоста. Кроме того, солнечная плазма достаточно свободно проникает в геомагнитосферу только в дальних (r > 150) областях хвоста и на замкнутые силовые линии она захватывается в основном в районе дальней (r ~ 150) нейтральной линии токового слоя (см. раздел 3.1.1). Поэтому на замкнутых силовых линиях реальной геомагнитосферы "рогатка" не срабатывает: частицы адиабатически замедляются [144] при вытягивании силовой трубки и во столько же раз ускоряются при ее сокращении (при этом потоки частиц будут постепенно уменьшаться и затем скачком восстанавливаться к исходным уровням или немного превышать их за счёт уплотнения плазмы в околополуночном секторе ПС [35, 42, 79]).
По-видимому, механизмы ускорения ионов до энергий КТ в авроральной области магнитосферы во время диполизации магнитного поля на взрывной фазе суббурь имеют в основном неадиабатический (стохастический) характер, что проявляется в суббуревых вариациях как формы спектров, так и питч-угловых распределений ионов.
Так, во время суббурь спектры ионов H+ и O+ ближнего ПС (r ~ 10¸ 11) почти не меняются в диапазоне E ~ 10¸ 60 кэВ, а при E > 60 кэВ они становятся более жёсткими: с увеличением энергии от ~ 60 до ~ 140 кэВ приращения потоков ионов во время типичной суббури увеличиваются на порядок величины [93]. Однако представленные в [93] данные противоречат предложенной там интерпретации: полагалось, что в результате ускорения скорости всех частиц увеличиваются на одинаковую величину. Это должно приводить к смягчению спектров (построенных в двойном логарифмическом масштабе), а наблюдался противоположный эффект. По оценкам магнитного поля ПС и характерных времён его изменения в [93] делается вывод, что условие адиабатичности нарушается для ионов O+ и сохраняется для протонов, но в эксперименте увеличиваются потоки как ионов O+, так и протонов, причём увеличение жёсткости их спектров примерно одинаковое.
Важно отметить, что аналогичные вариации ионных спектров наблюдались и во внешней (r ~ 6.6) части ловушки. По наблюдениям на ГСО слабые и умеренные суббури приводят к смягчению ионных спектров в диапазоне от нескольких десятков до нескольких сотен кэВ, а во время достаточно мощных суббурь и бурь спектры становятся жёстче [47, 61, 64, 65]. Суббуревой эффект смягчения ионных спектров в области ГСО можно объяснить механизмом диполизации магнитного поля. При этом чем больше начальная энергия частиц, тем скорее они покидают область ускорения и тем меньше относительное приращение их энергии (согласно проведённому в [145] моделированию скорости всех ионов увеличиваются на одинаковую величину). Это отвечает уменьшению D lnE с ростом E и - с учетом теоремы Лиувилля - смягчению спектров. Обратный эффект - увеличение жёсткости ионных спектров - можно объяснить с помощью стохастических механизмов ускорения ионов в ПС (см. раздел 3.2), что подтверждается наблюдениями в ближнем ПС [84, 93].
Расчёты показывают, что изменения конфигурации магнитосферы во время взрывной фазы суббури могут приводить к стохастическому ускорению вылетающих из ионосферы ионов O+ до ~ 80 кэВ в течение ~ 2 мин, причём эффективность такого ускорения максимальна вблизи внутренней границы авроральной области, т.е. в районе, сопряженном вдоль силовых линий магнитного поля с ГСО [146]. Эти выводы подтверждаются прямыми экспериментальными данными [31, 119].
Если вытягивание и последующее сокращение магнитных трубок авроральной области магнитосферы сопровождается питч-угловым рассеянием частиц, энергия плазмы перекачивается в ионные пучки, что наблюдалось во многих экспериментах. За несколько суббуревых циклов такой механизм может сформировать в ближнем ПС ионные пучки с энергией до нескольких десятков кэВ [147].
Для ионов с энергией менее нескольких кэВ при быстром втягивании магнитных силовых линий в ловушку может нарушаться инвариант I , что приводит к ускорению таких частиц, причём максимальное ускорение испытывают ионы с a 0 » 0, находящиеся в момент скачкообразных изменений полей вблизи экваториальной плоскости. Согласно модельным расчётам [28], ионы с E = 0.1 кэВ и a 0 = 5o увеличивают в эти моменты свою энергию в ~ 13 раз вблизи экватора и немного уменьшают её вблизи зеркальной точки, а ионы с a 0 = 90o увеличивают энергию всего в ~ 2.5 раза. Эффективность такого ускорения быстро уменьшается с ростом начальной энергии и при энергии более нескольких кэВ ионы ускоряются с сохранением как m , так и I , что приводит к противоположному результату: максимальное ускорение испытывают частицы с a 0 = 90o (бетатронный механизм). Рассмотренные эффекты приводят к формированию питч-угловых распределений ионов с отрицательной анизотропией (“сигарообразных”) при E < Es и с положительной анизотропией (“пончик”) при E > Es . Вблизи экваториальной плоскости такие вариации ионных распределений наблюдались на r ~ 6¸ 8 и было установлено: Es ~ 5¸ 6 кэВ для ионов H+ и ~ 12¸ 15 кэВ для ионов O+, что хорошо согласуется с расчётами [28].
Таким образом, согласно экспериментальным данным действующие в авроральной области магнитосферы суббуревые механизмы приводят к ускорению частиц и перераспределению их по питч-углам. При этом часть ионов высыпается в конус потерь и концентрация их в фазовом пространстве уменьшается. Однако при усреднении экспериментальных данных по LT и за продолжительные интервалы времени (несколько месяцев) суббуревые вариации формы спектров и распределений частиц по m (m > 0.1 кэВ/нТ), наблюдаемые в авроральной области магнитосферы, сглаживаются (см. результаты сравнения функций распределения ионов КТ и ПС в разделе 2). Это объясняется тем, что в отличие от бурь значительные суббуревые вариации спектров ионов с энергией более нескольких десятков кэВ имеют место только в узком околополуночном секторе (D LT ~ 2¸ 3 ч), а последующий дрейф частиц вокруг Земли приводит к быстрому (в течение десятков минут) выравниванию спектров.
Индукционные электрические поля, возникающие при коллапсировании магнитных полей, не нарушают скейлинг ионных спектров с x
i = Qi (но и не способствуют ему).Перестройка геомагнитного хвоста и связанные с ней резкие усиления электрического поля в околополуночном секторе магнитосферы приводят не только к ускорению частиц, но и к инжекции этих частиц в геомагнитную ловушку.
По данным геосинхронных и других спутников во внешней части ловушки и в ближнем ПС на
фазе роста суббури магнитные силовые линии вытягиваются в хвост магнитосферы и потоки частиц с энергией более нескольких десятков кэВ уменьшаются на 1¸ 3 порядка величины, а на взрывной фазе суббури магнитные силовые линии втягиваются в ловушку и потоки частиц увеличиваются на 2¸ 4 порядка величины в зависимости от вида частиц, их энергии, питч-угла и положения точки наблюдения [28, 80, 83].При втягивании силовых линий в ловушку ионы отклоняются на запад и инжектируются в вечерний и ночной сектора ловушки [5, 28]. По сравнению с ионосферными солнечные ионы инжектируются в ловушку немного восточнее и в более узком околополуночном секторе [60- 62]. В отличие от электронов значительная доля которых высыпается при этом в конус потерь, бó льшая (~ 90%) часть ионов удерживается в силовых трубках и втягивается в ловушку [79].
В различных областях внешней части ловушки всплески потоков частиц в начале взрывной фазы суббурь имеют различный характер: на большей части ГСО более энергичные частицы появляются раньше, а в предполуночные и утренние часы наблюдаются скачкообразные увеличения потоков частиц без дисперсии их по энергии [5, 28]. Этому эффекту отвечает суббуревая граница инжекции
- кратковременная резкая пространственная граница в ночной части ловушки, которая пересекает тем меньшие L чем ближе точка наблюдения к полуночному меридиану (ГСО она пересекает в вечернем секторе) и чем мощнее суббуря [5, 28]. Эта граница отвечает двум областям ближнего ПС с различными типами движения частиц: в области, примыкающей к ближней нейтральной линии токового слоя на r ~ 15 частицы подвергаются неадиабатическому ускорению, а ближе к Земле, в области достаточно сильного магнитного поля, неадиабатическое ускорение сменяется адиабатическим дрейфом частиц в магнитном и электрическом полях [137]. Резкий характер этой границы связан с тем, что после формирования на взрывной фазе суббури ближней нейтральной линии радиальный градиент магнитного поля резко увеличивается в этом районе.На главной фазе бури в результате инжекции горячей плазмы из ПС в вечернем секторе ловушки формируется асимметричный КТ. Последний инициирует процессы, приводящие к резкому усилению ионосферно-магнитосферных связей [114]. Благодаря азимутальным градиентам давления плазмы в ловушке генерируются биркеландовские токи, которые приводят к переформированию токовых систем и электрических полей в ионосфере. В свою очередь, ионосферные электрические поля проецируются в ловушку (вдоль магнитных силовых линий) и вызывают быструю (в течение 1¸ 2 ч) симметризацию КТ [114].
Косвенные проявления азимутальной асимметрии КТ наблюдались во многих спутниковых экспериментах. Так, во время бурь значительно возрастает азимутальная асимметрия депрессии магнитного поля D
B: вечером D B больше, чем утром [148]. Во время фазы восстановления гигантской бури 24 марта 1991 на L = 2¸ 4 в околополуночном секторе наблюдалось кратковременное обращение электрического поля с вечера на утро [57], что может быть связано с поляризацией асимметричного плазменного облака после затухания внешнего поля. Проявлением азимутальной асимметрии КТ можно считать и появление "носовых" структур в ионных спектрограммах КТ во время главной фазы бурь [7, 36, 42, 66].Небольшая асимметрия, связанная с асимметрией дрейфовых траекторий частиц и с диссипативными процессами в ловушке, характерна даже для спокойного КТ. Однако значительная азимутальная асимметрия КТ может развиваться только во время главной фазы бурь и для прямых оценок её величины необходимо проводить одновременные измерения потоков КТ в нескольких (разнесённых по LT) точках одной и той же дрейфовой оболочки. Это очень сложная техническая задача, не всегда разрешимая даже при наличии большого числа спутников. И только при очень редком благоприятном стечении обстоятельств возможно частичное разделение временнó го и пространственного эффектов нестационарного КТ (на главной фазе бури) по данным одного спутника. Такое разделение было проведено по данным Молнии-1 (с привлечением данных авроральных и субавроральных магнитных обсерваторий); по этим данным получены количественные оценки азимутальной асимметрии КТ [13, 14]. Долготная асимметрия буревого КТ обсуждалась также по данным
OGO-3 [3], но в этой работе не проводилось разделение временных и пространственных вариаций ионных потоков, а приведённые в [3] профили КТ (в дневной и ночной полусферах) относятся к разным суббурям и по ним нельзя судить о долготной асимметрии КТ.В связи с этим заметим, что по данным о магнитных возмущениях на низких и средних широтах азимутальная асимметрия КТ сильно преувеличена за счёт ионосферных токовых систем. Кроме того, асимметрия магнитного поля асимметричного КТ частично компенсируется противоположной по знаку асимметрией поля биркеландовских токов.
В [22] рассматривался магнитный эффект образующейся в околополуночном секторе во время суббурь токовой петли (частично-кольцевого тока): части этой петли с двумя продольными токами и ионосферным током восточного направления приводит к усилению магнитного поля на периферии ловушки и к его диполизации, способствуя тем самым проникновению в ловушку плотных сгустков горячей плазмы (с b > 1). К усилению и диполизации магнитного поля во внешних областях ловушки приводит и усиление КТ в её глубине, что также отмечалось в [22], т.е. чем глубже свежая горячая плазма внедряется в ловушку, тем более плотные потоки горячей плазмы могут проникать в ловушку на её периферии.
Исследования последних десятилетий свидетельствуют о неуниверсальности классической концепции бури как суперпозиции серии суббурь. Более того, на основе экспериментальных данных установлено, что бури могут развиваться и без суббуревого сопровождения. Так, на обс. Иркутск (
L = 2) во время сильной (maxç Dstç = 120 нТ) бури 18- 19 октября 1995 наблюдались редкие для таких широт очень сильные возмущения ионосферы и магнитного поля, причиной которых были не суббури, а перенос частиц ПС вплоть до L ~ 2 в условиях квазистационарной конвекции [149]. Однако, судя по быстрой (~ 18 ч) фазе восстановления этой бури, свежие частицы не удерживались геомагнитной ловушкой и возвращались в ПС (или выносились конвекцией из магнитосферы).Во время бурь концентрация ионов в ближнем ПС увеличивается до > 2 см-
3 [35, 42, 79]. При этом в околополуночном секторе на ГСО концентрация горячей плазмы увеличивается от 0.4¸ 2 до 2¸ 5 см- 3 [79]. Такое уплотнение ПС является необходимым условием формирования интенсивного КТ [39, 42, 150, 151].Большие магнитные бури (с
max½ Dst½ > 100 нТ) часто развиваются в две стадии (в начале фазы восстановления первой бури развивается следующая буря), которые отвечают двум близким изолированным интервалам с большой южной компонентой ММП [152, 153]. В результате математического моделирования динамики КТ во время таких событий показано [151], что для развития интенсивных бурь более глубокой инжекции КТ в ловушку, связанной с усилением глобального электрического поля (и амплитуды его флуктуаций) недостаточно и сам по себе факт двустадийности бури мало влияет на интенсивность КТ. Необходимо также значительное уплотнение ближнего ПС накануне бури. Такое уплотнение ПС реализуется к концу первой стадии двустадийных бурь и связано с активизацией ионосферного источника горячей плазмы или/и с разогревом ПС глобальным электрическим полем или/и с прохождением у границ геомагнитосферы плотных (20¸ 30 см- 3) сгустков плазмы солнечного ветра (магнитных облаков) в периоды, когда ММП направлено на юг. Поэтому сильные бури имеют либо продолжительную главную фазу (> 20 ч), либо развиваются в две стадии.Такие представления хорошо согласуются с результатами современных экспериментальных исследований, согласно которым сценарий суббури с околоземной нейтральной линией применим только к суббурям, развивающимся во время бури [90]: уменьшение магнитного давления в долях хвоста на взрывной фазе суббури наблюдается только для таких событий.
После инжекции в ловушку ионы КТ включаются в процесс конвекции в скрещенных магнитном и глобальном электрическом полях.
В отличие от вихревых электрических полей, масштаб потенциального электрического поля порядка размеров магнитосферы. Поскольку для этого поля магнитные силовые линии эквипотенциальны, оно проецируется из магнитосферы в ионосферу и формируется при участии ионосферно-магнитосферных связей (вихревые электрические поля не оказывают практически никакого влияния на ионосферу). Отвечающая этому полю разность потенциалов между утренним и вечерним флангами магнитосферы во время бурь достигает ~
100¸ 200 кВ [114].Согласно прямым измерениям на
L ~ 3¸ 7 вблизи экваториальной плоскости напряжённость глобального электрического поля составляет ~ 0.1¸ 0.2 мВ/м в спокойные периоды и ~ 1¸ 10 мВ/м во время бурь [154]. Косвенные оценки глобального электрического поля (по скорости движения полярных сияний на предварительной фазе суббури) дают следующие результаты [155]: в ближнем ПС это поле почти однородно, а от внешней границы ловушки его напряжённость быстро нарастает, достигая максимума на Lm ~ 6¸ 8; чем больше южная компонента ММП, тем глубже электрическое поле проникает в ловушку, больше его напряжённость и больше радиальные градиенты поля.На внутренней кромке КТ электростатическое поле сильнее, чем на его внешней кромке, причём область максимального усиления этого поля совпадает с областью максимального усиления потоков КТ (придвигаясь к Земле с ростом
Kp и Dst); этот эффект максимален в вечернем секторе и начинает проявляться уже при Kp = 3¸ 4, увеличиваясь с ростом Kp [56]. Так, во время гигантской бури 24 марта 1991 (max½ Dst½ ~ 300 нТ) электростатическое поле проникало до L ~ 2 и достигало 8 мВ/м, а на L > 4 оно не превышало 1¸ 2 мВ/м; в конце главной фазы этой бури максимальная депрессия магнитного поля в ловушке, связанная с КТ, составляла 350 нТ и локализовалась на L = 2.4 - там же, где и максимум электростатического поля [57]. На главной фазе этой бури такие большие электростатические поля держались несколько часов и могли инжектировать ионы с L = 8 на L = 2.4, адиабатически ускоряя их при этом от 1¸ 5 до 300 кэВ.В некоторых областях магнитосферы и в определённые периоды времени (в околополуночном секторе авроральной области во время взрывной фазы суббури и в околополуденном секторе во время сильных поджатий магнитопаузы) вихревые поля могут значительно превышать рассматриваемое поле. Кратковременное (в течение нескольких минут) суббуревое возрастание вихревого электрического поля до 20 мВ/м в полуночном секторе наблюдалось даже на
L = 3.5¸ 6.5 [57]. Однако локальные индукционные поля не отменяют глобальное электрическое поле и вызываемую им конвекцию горячей плазмы во внутренних областях магнитосферы. Вихревые электрические поля вызывают быстрые локальные вариации потоков частиц, но в ходе дрейфа частиц эти вариации сглаживаются и усреднённые пространственно-энергетические распределения КТ и ближнего ПС хорошо описываются моделями конвекции [36, 40, 66].Для описания конвекции горячей плазмы в ловушке используется модель электрического поля Волланда-Стерна [156]:
U = U0 Lpsin(j - j 0) - UW L- 1,
где
U - потенциал поля, j - долгота (отсчитывается от полуночного меридиана на восток) и j 0 - компенсирующий угол. Первый член этого выражения описывает поле конвекции (зависимость его от уровня геомагнитной активности учитывается в коэффициенте U0), второй - постоянное радиальное поле, которое генерируется в результате вращения Земли (UW = const). Показатель p, учитывающий экранировку электрического поля плазмосферой, задаётся в пределах от 1 до 3 (при увеличении p экранировка усиливается). Динамика спектров ионов КТ лучше всего описывается при p ~ 2 и j 0 ~ 30¸ 45o [36, 66].Переменная часть (флуктуации) глобального электрического поля не экранируется плазмопаузой [157] и при моделировании с учётом нестационарной конвекции (диффузии) ансамбля частиц в ловушке к правой части приведённого выражения добавляют член, который описывает изменяющееся, но однородное поле, направленное с утра на вечер [39, 55, 59, 112, 151].
Основные закономерности конвекции горячей плазмы во внешней части ловушки, установленные в теоретических работах, подтверждаются прямыми экспериментальными данными. Так, внутренняя граница области конвекции
(альвеновский слой), за которой глобальное электрическое поле резко ослабляется (экранируется), примерно совпадает с усредненным по LT положением плазмопаузы и внутренней кромкой КТ; во время главной фазы бури эти границы синхронно смещаются на меньшие L, причём перекрытие КТ с плазмосферой в эти периоды не превышает 0.5 RE [4, 7, 57, 58].Конвекция проявляется также в особенностях буревой пространственно-энергетической структуры потоков ионов в сердцевине ловушки [7], в суточном ходе основных параметров ионного КТ
на ГСО [60, 61, 64] и во многих других экспериментальных данных.В спектрах ионов КТ конвекция проявляется не только вблизи экваториальной плоскости, но и на средних широтах [17, 66], а также на высотах полярных спутников [158]. Так, по данным Молнии-1
(l ~ 20¸ 50o) проведен сравнительный количественный анализ влияния конвекции и питч-угловой диффузии (высыпания) протонов под действием циклотронной неустойчивости на формирование азимутальной асимметрии КТ [17].В рамках модели нестационарной конвекции плазмы в ограниченной слабодиссипативной системе с полупрозрачными стенками можно объяснить скейлинг ионных спектров КТ с x
i = Qi в диапазоне E/Qi от нескольких десятков до нескольких сотен кэВ [102, 103].Поскольку электрическое поле сильно флуктуирует, особенно во внешней части ловушки и в ближнем ПС (с удалением точки наблюдения от Земли амплитуды этих флуктуаций увеличивается и в ближнем ПС она достигает величины среднего поля или даже превышают эту величину), реальные траектории отдельных частиц воспроизводят броуновское движение и не похожи на гладкие кривые, которыми изображаются конвективные потоки. Поэтому всё, что говорится о конвекции горячей плазмы в магнитосфере, надо понимать как описание средних характеристик потоков и распределений частиц, причём хотя движение отдельных частиц КТ и ближнего ПС нерегулярно, результаты [49, 50, 99- 103, 109] свидетельствуют, что инварианты m и I ионов при этом в среднем сохраняются. Фактически такая картина конвекции подразумевалась в [39, 55, 59, 111, 151]. При таком понимании классическая концепция конвекции применима не только во всех областях геомагнитной ловушки за плазмопаузой, но и в ближнем ПС (в области замкнутых силовых линий), т.е. справедлива для геокороны горячей плазмы в целом.
Глобальное электрическое поле и связанная с ним конвекция горячей плазмы проявляются и в ближнем ПС [25, 40, 86, 90], причём по экспериментальным данным диполизация магнитного поля и направленная к Земле конвекция в ближнем ПС сильнее выражены для суббурь, развивающихся на главной фазе бури [90]. Численное моделирование траекторий нерелятивистских частиц в ближнем ПС также показывает, что несмотря на хаотичность движения в случае, когда скорости дрейфа малы по сравнению со скоростями частиц (это обычно выполняется), перенос частиц можно описывать в адиабатическом дрейфовом приближении [159].
Конвективные вихри в ПС могут простираться до точки застоя на
r ~ 45 [95]. Однако в достаточно удаленных от Земли областях ПС суббуревая динамика потоков и спектров горячей плазмы плохо описывается дрейфовыми (конвективными) моделями, что проявляется, например, в результатах Galileo [95]; в этих областях конвекция реализуется в виде кратковременных (несколько минут) дискретных струй высокоскоростных (до 2000 км/с) потоков горячей плазмы [91].Ионный КТ распадается в результате взаимодействия ионов с атомами экзосферы и с холодной плазмосферной плазмой (ионизационные потери), а также - с волнами. Ионизационные потери ионов КТ складываются из перезарядки ионов с атомами экзосферы и кулоновского торможения ионов в плазмосфере и во внешних областях экзосферы. Для времени жизни КТ важны только низкочастотные (в основном циклотронные) электромагнитные волны (ионно-циклотронная неустойчивость КТ); эти волны приводят к питч-угловой диффузии ионов КТ в конус потерь.
В условиях геомагнитной ловушки кулоновское потери энергии нужно учитывать только для ионов очень малых и достаточно больших энергий, а в промежуточном энергетическом интервале ионизационные потери почти полностью определяются перезарядкой (например, для протонов перезарядка вносит основной вклад при 7 < E < 200 кэВ, а при меньших и бó льших энергиях доминирует кулоновское торможение [41]). Слабые процессы перезарядки ионов проявляется даже в ближнем ПС [40]. Параметры наблюдаемого в спокойные периоды на L < 5 провала в ионных спектрах КТ при E/Qi ~ 20¸ 100 кэВ [6, 10, 32] - его глубина, форма и положение по энергетической шкале на разных L - хорошо согласуются с расчётными значениями, полученными с учётом баланса процессов обновления частиц в ловушке (в основном в результате радиальной диффузии) и процессов ионизационных потерь (в основном перезарядки) [36, 38, 41].
Циклотронные волны в геомагнитной ловушке генерируются ионами примерно того же энергетического диапазона, в котором доминирует перезарядка, при достаточно большой величине положительной анизотропии и достаточно высоких уровнях потоков частиц [11, 15].
В спокойные периоды максимум дифференциальной плотности энергии КТ приходится на протоны с Е ~ 200 кэВ (75% полной энергии КТ приходится на протоны с Е ~ 100¸ 400 кэВ), а во время бурь - на ионы с Е/Qi ~ 50¸ 100 кэВ (90% полной энергии КТ приходится на ионы с E/Qi ~ 10¸ 200 кэВ) [6, 11, 32]. Поэтому характерные времена жизни ионов КТ в спокойные периоды и во время слабой магнитной активности определяются кулоновским торможением и перезарядкой [38, 41], а во время типичных бурь - перезарядкой ионов [10, 38, 40, 41] и циклотронной неустойчивостью КТ [11].
Для типичных бурь расчётные времена распада ионного КТ, отвечающие процессам перезарядки и питч-угловой диффузии ионов под действием циклотронных волн, примерно одинаковы. Но при этом следует учитывать, что с уменьшением потоков ионов КТ режим генерации циклотронных волн может поддерживаться только за счёт роста анизотропии потоков и этот рост обеспечивается благодаря непрерывно идущим процессам перезарядки ионов. Поэтому при анализе основных закономерностей затухания КТ на фазе восстановления типичных бурь можно ограничиться рассмотрением только процессов перезарядки ионов.
На данной L-оболочке КТ затухает в результате перезарядки ионов с постоянной времени ![]() , где nH(L) -
концентрация атомов водорода (основного атомарного компонента на высотах КТ), а
, где nH(L) -
концентрация атомов водорода (основного атомарного компонента на высотах КТ), а ![]() и
и ![]() -
усреднённые по энергии эффективные величины сечения перезарядки и скорости ионов (бó
льшая часть ионов КТ имеет a
0 = 90 ±
30o и изменение концентрации водорода вдоль магнитной силовой линии при таком анализе можно не учитывать). Для различных ионных компонентов КТ величины
-
усреднённые по энергии эффективные величины сечения перезарядки и скорости ионов (бó
льшая часть ионов КТ имеет a
0 = 90 ±
30o и изменение концентрации водорода вдоль магнитной силовой линии при таком анализе можно не учитывать). Для различных ионных компонентов КТ величины ![]() существенно различаются; для ионов группы CNO с Qi = + 1 величины
существенно различаются; для ионов группы CNO с Qi = + 1 величины ![]() значительно меньше, чем для протонов.
значительно меньше, чем для протонов.
Связанное с перезарядкой время жизни ионного КТ (как целого) определяется двумя конкурирующими эффектами: а) с уменьшением L растёт nH(L) и, следовательно, ![]() уменьшается; б) чем ближе КТ подходит к Земле, тем больше средняя энергия составляющих его ионов (бетатронное ускорение) и больше время их жизни. При достаточно быстром уменьшении s
ce с ростом энергии частиц второй эффект будет доминировать.
уменьшается; б) чем ближе КТ подходит к Земле, тем больше средняя энергия составляющих его ионов (бетатронное ускорение) и больше время их жизни. При достаточно быстром уменьшении s
ce с ростом энергии частиц второй эффект будет доминировать.
Будем полагать, что с уменьшением L концентрация атомов водорода увеличивается как L-
4. Поскольку бó
льшая часть ионов КТ имеет a
0 = 90 ±
30o, средняя энергия ионов увеличивается как L-
3, а средняя скорость -
как L-
3/2. Сечение перезарядки максимально при E/Mi ~
10 кэВ, а при бó
льших энергиях s
ce быстро уменьшается и можно использовать аппроксимацию s
ce µ
E-
m [10], т.е. ![]() µ
L3m и, следовательно,
µ
L3m и, следовательно, ![]() . При m > 11/6 »
2 время жизни ионов КТ (на данной L) увеличивается с уменьшением L. Для ионов H+ m »
2.6 при E »
30¸
80 кэВ и m »
4.3 при E > 80 кэВ; для ионов He2+ m »
2.6 при E/Mi »
50¸
130 кэВ и m »
4.3 при E/Mi > 130 кэВ; для ионов O+ m »
0.6 при E > 20 кэВ [10, 41].
. При m > 11/6 »
2 время жизни ионов КТ (на данной L) увеличивается с уменьшением L. Для ионов H+ m »
2.6 при E »
30¸
80 кэВ и m »
4.3 при E > 80 кэВ; для ионов He2+ m »
2.6 при E/Mi »
50¸
130 кэВ и m »
4.3 при E/Mi > 130 кэВ; для ионов O+ m »
0.6 при E > 20 кэВ [10, 41].
Для той части ионов H+ и He2+, на которую приходится максимум плотности энергии КТ, m > 2 и среднее значение m ~ 3.5. Следовательно, для бурь с max½ Dst½ < 200 нТ, когда основной вклад в энергию КТ вносят протоны, продолжительность фазы восстановления тем больше, чем глубже КТ внедряется в ловушку. Однако для более сильных бурь, в начале которых основной вклад в энергию КТ могут вносить ионы O+, рассмотренная зависимость может быть обратной: чем глубже КТ внедряется в ловушку, тем быстрее вымирают ионы O+.
При моделировании потерь энергии КТ на фазе восстановления умеренных бурь в [42] в дополнение к перезарядке (основные потери) и кулоновскому торможению ионов учитывалось высыпание ионов. Имелось в виду не высыпание в конус потерь в результате питч-угловой диффузии частиц под действием волн [11], а высыпание, связанное с конвекцией: при адиабатическом (m
,I = const) переносе частиц с достаточно малыми экваториальными питч-углами a 0 на меньшие L точки их отражения понижаются и достигают границы атмосферы [160]. В некоторые периоды бурь вклад такого механизма в потери энергии КТ приближается к вкладу кулоновского торможения ионов [42]. Поскольку в таком механизме интенсивность высыпания должна увеличиваться с ростом электрического поля конвекции, этим может объясняться (хотя бы частично) хорошо известная корреляция потоков высыпающихся ионов с Kp: с ростом Kp поле конвекции усиливается (перезарядка и кулоновское торможение не могут отвечать за такую корреляцию).Особый интерес представляют гигантские бури (
max½ Dst½ > 300 нТ) с типичной для них двустадийной фазой восстановления: быстрая начальная стадия продолжается несколько часов, а медленная завершающая - несколько недель.В настоящее время наиболее подробно изучена эволюция КТ во время гигантской бури в феврале 1986, к концу главной фазы которой сформировался КТ с максимумом плотности энергии на
L ~ 2.6 [35]. Быстрая стадия фазы восстановления этой бури связывалась в [35] в основном с распадом кислородного компонента КТ (продолжительность этой стадии отвечает временам перезарядки ионов O+ c E ~ 10¸ 200 кэВ на L ~ 2.5¸ 3.5 и ионов H+ с E ~ 20¸ 50 кэВ на L ~ 2.5¸ 3.0, а последующая медленная стадия - с кулоновским торможением ионов (с энергией от нескольких сотен кэВ до нескольких МэВ), а также с перезарядкой ионов H+ меньших энергий.Временной ход
Dst на фазе восстановления нескольких гигантских бурь анализировался также в [45, 153]. В этих работах гигантские бури связывались с инжекцией в ловушку ионов O+, начальная быстрая стадия фазы восстановления - с распадом кислородного компонента КТ, а последующая медленная стадия - с распадом протонного компонента КТ.Однако более тщательные модельные расчёты показывают, что при учёте только ионизационных потерь ионов нельзя объяснить количественно ни быструю стадию фазы восстановления, ни резкого уменьшения скорости распада КТ в начале медленной стадии фазы восстановления бури в феврале 1986 [43]. В этой работе анализировались синхронные данные трёх спутников и в расчётах использовалась наиболее современная модель эволюции КТ, учитывающая перезарядку и кулоновское торможение ионов. Показано, что обновлением КТ на фазе восстановления указанной бури можно пренебречь и экспериментальные данные согласуются с расчётами только при следующих предположениях [43]: на быстрой стадии скорости диссипации энергии КТ за счёт перезарядки ионов O
+ и за счёт высыпания частиц в конус потерь при взаимодействии с волнами сопоставимы друг с другом, а на медленной стадии основным механизмом становится перезарядка ионов, причём перезарядка ионов O+ продолжает играть важную роль в течение ещё трёх дней.В качестве основной причины быстрой стадии фазы восстановления гигантских бурь рассматривались также сильная питч-угловая диффузия и высыпание ионов КТ в конус потерь при взаимодействия их с циклотронными волнами [66] и быстрый распад внутренней части токового слоя магнитосферного хвоста [161]. Внезапный поворот ММП на север (это происходит обычно в конце главной фазы или в самом начале фазы восстановления бури) может приводить к внезапному резкому ослаблению или даже к обращению глобального электрического поля, что способствует выталкиванию КТ из внешних областей ловушки и также может быть причиной быстрой фазы восстановления бурь [54, 150].
Большой интерес представляют задачи, связанные с изучением механизмов диссипации КТ на главной фазе бурь. Показано, что на главной фазе гигантских бурь время распада КТ определяется в основном сильной питч-угловой диффузией и конвективным выносом частиц КТ к дневной магнитопаузе и составляет ~ 1 ч [1
52].В заключение этого раздела заметим, что кроме циклотронных, в геомагнитной ловушке генерируются также электромагнитные волны более низких частот (в диапазонах Pc 3¸ 5). Эти волны не оказывают значительного влияния на равновесие КТ в целом, но могут вызывать значительные (до порядка величины) кратковременные (от нескольких десятков минут до нескольких часов) квазипериодические вариации потоков частиц КТ во внешней части ловушки. При определённых условиях такие волны могут вступать в резонанс с ионами КТ и формировать локальные особенности в их распределениях. Так, по данным геосинхронного спутника Горизонт-35 во время сильных магнитных возмущений в спектрах ионов (H
+, He2+ и O+) КТ формировался монохроматический пик при E/Qi » 130 кэВ; такой пик может возникать в результате резонанса ионов с дрейфовыми (Pc 4¸ 5) волнами в области ГСО, где складываются наиболее благоприятные для такого резонанса условия [63].Напомним, что планетарный КТ был введен для объяснения Dst-
вариаций (усредненных по долготе вариаций магнитного поля по данным низкоширотных обсерваторий) во время геомагнитных бурь [1]. По современным представлениям, кроме КТ в Dst вносят вклад также токи на магнитопаузе (поджатие магнитопаузы солнечным ветром) и токи в нейтральном слое геомагнитного хвоста. Вклад КТ в Dst будем обозначать как ![]() .
.
Аналитические вычисления магнитного эффекта КТ проводились только для дипольного магнитного поля и в линейном приближении: обратным влиянием поля КТ на движение его частиц пренебрегалось [162, 163]. При этих условиях получено простое соотношение между величиной
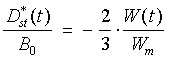 ,
,
где
Магнитное поле КТ находилось также на основе более общих выражений для тока захваченных частиц, учитывающих как магнитный дрейф, так и ларморовское вращение частиц (диамагнитную компоненту тока), что также доказывает справедливость формулы DPS [164].
Коэффициент 2/3 в этой формуле учитывает магнитные поля индукционных токов в земной коре, экранирующих поля внешних токовых систем (диамагнитный эффект). В [162,163] Земля рассматривалась как идеальный диамагнетик; в этом случае внешние магнитные поля не проникают внутрь Земли (полностью экранируются). В действительности Земля не является идеальным диамагнетиком и указанный коэффициент ближе к 0.77 [165]. С учетом этой поправки вклад магнитного поля КТ в
Dst составляет следующую величину:Средние энергии электронов и ионов КТ практически совпадают, но взаимодействия частиц с волнами ограничивают концентрацию электронов КТ гораздо более низким по сравнению с ионными критическим уровнем. Поэтому магнитный эффект КТ во время бурь определяется в основном ионами (квазинейтральность плазмы обеспечивается притоком холодных ионосферных электронов).
Формула DPS проверялась по данным
OGO-3 [2], Explorer-45 [8], Молния-1 [16], AMPTE/CCE [33, 35, 39, 43, 46] и др. Для этих данных формула DPS достаточно хорошо описывает Dst- вариацию во время бурь разной силы; радиальные профили плотности энергии ионов КТ и локальной депрессия магнитного поля также хорошо согласуются друг с другом. Относительный вклад в Dst и возмущения магнитного поля во внутренней части ловушки ионного КТ составляет > 50% даже во время гигантских бурь [43].Токи на магнитопаузе вносят положительный вклад в
Dst , который пропорционален квадратному корню из динамического давления солнечного ветра [152, 167, 168], т.е.![]() .
.
В [167] для
b и c были получены значения 16 нТ/нПа1/2 и 20 нТ, а при более полном анализе экспериментальных данных, учитывавшем независимость среднестатистической величины Psw от Dst и VswBsw , для b и c получено 7.26 нТ/нПа1/2 и 11 нТ [168].Из этих результатов следует, что эффект поджатия магнитопаузы сильно ослабляется в глубине магнитосферы: величина коэффициента
b = 16 нТ/нПа1/2 [167] отвечает ослаблению граничного возмущения геомагнитного поля в магнитосфере (от магнитопаузы к поверхности Земли) в ~ 3 раза, а более реалистичное значение b = 7.26 нТ/нПа1/2 - в ~ 7 раз. Это связано с тем, что в ходе поджатия поля захваченные в геомагнитной ловушке частицы подвергаются бетатронному ускорению и давление их возрастает в такой же пропорции как и давление локального магнитного поля. В результате магнитный эффект поджатия магнитопаузы частично компенсируется в ловушке (диамагнетизм); чем ближе точка наблюдения к Земле и чем интенсивнее КТ, тем компенсация полнее. Относительный вклад этого эффекта в Dst не превышает 20% [43].Отрицательный вклад в
Dst вносит также токовый слой геомагнитного хвоста [161, 169]. Однако этот вклад не превышает, по-видимому, 20¸ 30% от вклада КТ для гигантских и 10¸ 20% - для обычных бурь. В связи с этим заметим, что в [169] была предложена альтернативная теория, согласно которой буревые вариации Dst в основном отражают усиление токов нейтрального слоя магнитосферного хвоста и магнитный эффект КТ почти полностью компенсируется поджатием магнитопаузы. Однако в этой работе недооценивается ослабление эффекта поджатия магнитопаузы в глубине магнитосферы, и тем самым сильно переоценивается вклад в Dst токов на магнитопаузе. Фактически в [169] полагается, что инжекции горячей плазмы в ловушку синхронизована с поджатием магнитосферы и последний эффект полностью отвечает за увеличение полной энергии КТ во время бурь.На Земле эффект поджатия магнитосферы проявляется в импульсах
SC и SI, типичная амплитуда которых составляет от нескольких нТ до нескольких десятков нТ. Однако многие, даже очень мощные, бури развиваются без SC. Кроме того, отвечающее SC поджатие магнитопаузы продолжается несколько десятков минут, а главная фаза бури, когда в ловушку инжектируются частицы КТ, - несколько часов или десятки часов, т.е. SC намного короче главной фазы бури. Быстрая фаза восстановления бури связывается в [169] с адиабатическим замедлением частиц КТ после снятия повышенного давления на магнитосферу, но эта фаза имеет место только для бурь с max½ Dst½ > 150 нТ и хорошо объясняется распадом КТ [35, 43, 45, 153], а также - внутренней части токового слоя магнитосферного хвоста [161].Попытка кардинального реформирования традиционных представлений о механизмах генерации токовых систем и связанных с ними магнитного и электрического полей в геомагнитной ловушке и ближнем ПС предпринята в [170- 173] и в других работах этих авторов; подробное рассмотрение этих работ было бы весьма поучительно, но за неимением места ограничимся здесь только некоторыми краткими комментариями по этому поводу.
Рассматривавшееся в [171- 173] хорошо известное ветвление дрейфовых оболочек во внешней части ловушки [164] по существу ничего не меняет в наших представлениях о связи КТ с величиной
Dst: ветвление оболочек ("разрезной КТ" [171- 173]) отвечает "бабочкообразным" ПУР частиц в дневной части ловушки, но в [163] показано, что формула DPS справедлива для любых ПУР частиц КТ.В [171- 173] "истинный" радиальный профиль давления буревого КТ находился как разность буревого и спокойного профилей давления КТ. В результате такой процедуры внутренняя кромка КТ во время бурь значительно отодвигается от Земли (во внешнюю область ловушки). Эти рассуждения некорректны, поскольку инжекция горячей плазмы сопровождается ослаблением магнитного поля ловушки и адиабатическим замедлением частиц РП (спокойного КТ): вычитать надо не давление спокойного КТ, а исправленное на адиабатический эффект давление РП. В результате расчётов учитывающих адиабатический эффект и реальные спектры частиц получаются "истинные" радиальные профили давления буревого КТ, которые немного отличаются от экспериментальных профилей буревого КТ во время слабых бурь и практически совпадают с экспериментальными во время сильных бурь (
max½ Dst½ > 150 нТ).Применявшаяся в [171- 173] стратегия поиска "истинного" радиального профиля давления буревого КТ приводит к концепции гипотетического восточного КТ на периферии ловушки. В этих работах полагается, что во время бурь такой ток задаёт движение магнитопаузы к Земле и является (вместе с "разрезным" КТ) ключевым элементом нового механизма суббурь. Однако концепция восточного КТ не только противоречит реальным распределениям горячей плазмы во внутренней магнитосфере (см. выше), но и внутренне противоречива: связанное с восточным током вытягивание магнитных силовых линий в хвост приведёт к резкому уменьшению давления плазмы (в связи с её адиабатическим охлаждением и разрежением) и уменьшению западного диамагнитного тока (а также западного дрейфового тока) в примыкающих к восточному току областях хвоста, что будет гасить рассматривавшиеся в [171- 173] эффекты на стадии их зарождения.
Во время магнитных активизаций на периферии ловушки и в ближнем ПС (на
r от ~ 5¸ 8 до ~ 15 и более) радиальный градиент давления плазмы вблизи полуночного меридиана мал. Однако отсюда не следует, как утверждается в [171- 173], что в эти периоды градиент давления на внешней кромке глобального КТ близок к нулю и доминирует направленный на восток диамагнитный ток, отвечающий внутренней кромке КТ, т.е. суммарный азимутальный ток в ловушке меняет направление с западного на восточное. Поскольку в магнитно-активные периоды дрейфовые траектории частиц разомкнуты на r > 5¸ 6, после интегрирования энергии частиц по дрейфовым оболочкам (для всех значений LT) получаем радиальный ход, который имеет отрицательный градиент и резко обрывается у внешней границы ловушки [8, 16, 17, 29, 33]. Поэтому суммарный западный ток в геомагнитной ловушке, связанный с магнитным дрейфом частиц и отрицательным радиальным градиентам давления плазмы на внешней кромке КТ, всегда значительно превышает (в соответствии с формулой DPS) восточный ток, отвечающий внутренней кромке КТ. В [150] магнитное поле КТ находилось путём прямых вычислений интеграла Био-Савара. Результаты этих расчётов совпадают с формулой DPS и хорошо описывают Dst- вариацию во время конкретных бурь, причём в [150] показано, что во время трёх бурь различной интенсивности КТ на L > 4¸ 5 был направлен на запад и значительно превышал восточный ток на внутренней кромке КТ.На главной фазе бури, когда развивается асимметричный КТ, генерирующий мощные биркеландовские токи [114], условия применимости формулы DPS не выполняются. Если же КТ генерирует значительные биркеландовские токи, которые согласно модели [170] сопоставимы с экспериментальными величинами токов зоны 1, и на фазе восстановления бури (а также в спокойные периоды) - формула DPS неприменима и к этим периодам (биркеландовские токи частично компенсируют вклад КТ в величину
Dst), что не соответствует действительности. Однако если аккуратно просчитать трансформацию полной функции распределения в ходе дрейфа частиц в асимметричной ловушке, то в каждой из силовых трубок число приходящих и уходящих частиц будет, по-видимому, полностью сбалансировано (для стационарного КТ).Представленные в [174] модели магнитного поля симметричной и асимметричной составляющих КТ (по данным
AMPTE/CCE) показывают, что величины биркеландовских токов, связанных с азимутальной асимметрией давления плазмы в геомагнитной ловушке, значительно меньше величин наблюдаемых на малых высотах продольных токов (по крайней мере в спокойные периоды); показано, что даже токи зоны 2 (внутренней по отношению к зоне 1) формируются вне ловушки - в ближнем ПС.В [171- 173] совершенно игнорируются токи, связанные с магнитным дрейфом частиц и полагается, что как КТ, так и ток в ПС связаны только с градиентами давления плазмы. Такие упрощённые представления справедливы для равновесных магнитостатических систем, к которым стремятся (как к идеальным условиям удержания плазмы) в лабораторных установках, но реальная магнитосфера принципиально неравновесна и магнитостатика к ней по-видимому неприменима.
С проблемой магнитного поля КТ связана проблема разделения буревых вариаций потоков и спектров частиц РП на адиабатическую и неадиабатическую составляющие. Судя по экспериментальным данным, область, в которой потоки частиц испытывают во время бурь чисто адиабатические вариации, занимает весьма ограниченную часть пространства {
E,a 0,L}, причём границы этой области и ее конфигурация неуниверсальны (определяются характеристиками конкретной бури).Для выделения адиабатической составляющей вариаций потоков и спектров частиц необходима привязка их к магнитным силовым трубкам и дрейфовым оболочкам, что возможна только при наличии синхронной информации о вариациях поля в ловушке, полученной с высоким пространственным разрешением (по одновременным измерениям в достаточно большом числе точек). До настоящего времени такие подробные эксперименты не проводились и в обозримом будущем они вряд ли будут реализованы.
В ряде работ буревые вариации магнитного поля в ловушке оценивались по индексу
Dst с помощью теоремы DPS. Однако простая линейная зависимость между магнитным полем КТ и полной кинетической энергией частиц КТ (теорема DPS) справедлива только для усреднённых по долготе наземных измерений низкоширотных вариаций магнитного поля (Dst) или в центре КТ. В других точках ловушки магнитный эффект КТ зависит не только от полной энергии, но и от пространственного распределения частиц КТ. Кроме того, теорема DPS учитывает только КТ и полностью игнорирует другие токовые системы (биркеландовские, ионосферные, в магнитосферном хвосте и на магнитопаузе), которые могут пересиливать магнитное поле КТ во внешних областях ловушки в периоды магнитных активизаций; не учитывает она и локальные вариации давления плазмы в ловушке, что также приводит к большим методическим ошибкам.Поэтому неудивительно, что выводы [175] о величине буревой депрессии магнитного поля в ловушке, полученные из анализа экспериментальных данных о РП с помощью теоремы DPS, опровергались результатами совместного анализа данных спектрометра протонов с
E = 1¸ 800 кэВ и высокочувствительного магнитометра на ИСЗ Explorer-45 [9]; для рассмотренной в [9] бури депрессия магнитного поля, вычисленная методом [175], значительно меньше экспериментальных величин (во время главной фазы бури - в ~ 5 раз).В результате проведённого в [175] анализа сделан общий вывод: во время бурь потоки захваченных ионов с энергией более нескольких сотен кэВ испытывают в основном адиабатические вариации. Однако другие исследования показывают, что это правило неуниверсально и часто нарушается. Так, во время бури с необычным триггером наблюдалось формирование нового пояса протонов с энергией до нескольких десятков МэВ на
L < 2 [176], а на L > 2.4 вариации потоков даже очень энергичных (Е = 40¸ 110 МэВ) протонов РП имеют неадиабатическую составляющую и во время обычных (достаточно сильных) бурь [177]. На основе инвариантного представления и законов скейлинга энергетических спектров ионов (см. раздел 2.1) предложены более простые методы выделения и количественного анализа адиабатической составляющей буревых вариаций потоков и спектров ионов в геомагнитной ловушке для диапазона m /Qi ~ 1¸ 10 кэВ/нТ по спутниковым данным [178].В сердцевине ловушки и у внешней ее границы (в области ГСО) временные вариации потоков и спектров ионов с
E/Qi > 20 кэВ в магнитно-активные периоды имеют принципиально различный характер. В сердцевине ловушки потоки ионов с E/Qi от нескольких десятков до нескольких сотен кэВ существенно возрастают, а при бó льших энергиях - уменьшаются, т.е. спектры становятся мягче. Однако в области ГСО увеличение потоков ионов охватывает гораздо более широкий энергетический диапазон (от нескольких кэВ до нескольких МэВ). Кроме того, в районе ГСО потоки частиц (а также магнитное поле) восстанавливаются гораздо быстрее, чем в сердцевине ловушки. В сердцевине ловушки потоки ионов с E/Qi < 100 кэВ коррелируют, а ионов с E > 100 кэВ хорошо антикоррелируют с ½ Dst½ . Этот эффект очень чётко проявляется во время бурь с max½ Dst½ > 100 нТ, когда КТ инжектируется до L < 3¸ 4 [9, 175]. Однако в области ГСО потоки ионов с E/Qi > 40 кэВ практически не коррелируют с Dst, хотя и проявляется довольно чёткая корреляция их с индексами AE и Kp [51, 62].Такие различия связаны с различием времён переноса частиц от границы захвата (из ПС) на разные
L: в область, непосредственно примыкающую к границе захвата (на L ~ 6¸ 7), возможна быстрая инжекция частиц практически любых энергий, а времена переноса частиц больших и малых энергий на L < 5 различаются на несколько порядков величины. Во время бурь конвективный перенос ионов с E/Qi < 100 кэВ в глубь ловушки реализуется за десятки минут, что вызывает локальную депрессию магнитного поля и адиабатическое уменьшение потоков более энергичных захваченных частиц, которые обновляются там гораздо более медленной радиальной диффузией. Кроме того, следует иметь в виду, что во время типичных магнитных возмущений почти все частицы КТ в сердцевине ловушки удерживаются на замкнутых дрейфовых оболочках, а в районе ГСО только небольшая доля частиц промежуточных энергий (несколько сотен кэВ) имеет устойчивые замкнутые траектории; остальные частицы дрейфуют по разомкнутым или неустойчивым траекториям и для них эта область является зоной квазизахвата.В настоящее время твёрдо установлено, что в магнитосфере бó льшая часть энергии солнечного ветра сначала запасается в виде магнитной энергии долей хвоста и только после этого преобразуется, спонтанно или вынужденно, в энергию частиц горячей магнитосферной плазмы и другие формы энергии. Эти процессы не обязательно должны идти одновременно и могут иметь разные характерные скорости. При резком нарушении баланса этих скоростей магнитосфера переходит в новое состояние с минимумом свободной энергии (в результате развития суббури).
Во время бурь нарушается баланс процессов инжекции и диссипации плазмы КТ: на главной фазе пересиливает инжекция, а на фазе восстановления - диссипативные процессы. Такая ситуация описывается простым дифференциальным уравнением, если задавать инжекцию оператором, зависящим только от параметров солнечного ветра. Для этого необходимо исключить из рассмотрения спонтанные суббури и сгладить по времени эффект вынужденных суббурь. В связи с этим отметим, что хотя суббури сопровождаются значительными быстрыми вариациями потоков частиц не только в ПС, но и в околополуночном секторе внешней части ловушки, на фазе восстановления бури развиваются, по-видимому, только спонтанные суббури, которые не оказывают существенного влияния на основную часть КТ [153]. Суббури, развивающиеся на главной фазе бури, обеспечивают быструю инжекцию горячей плазмы в КТ, но если такие суббури вынужденные - можно полагать, что и на главной фазе бури состояние КТ в целом контролируется солнечным ветром.
Тогда скорость изменения полной энергии КТ (W) равна разнице между мощностью источников КТ (S) и скоростью диссипации энергии КТ. Если полагать, что последняя характеризуется временем t (это сильное упрощение), то
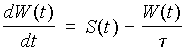 .
.
Заменяя
W(t) на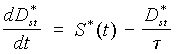 . (1)
. (1)
Величина
 ,
,
где
a » - 5 (нТ/ч)(мВ/м)- 1, Ec » 0.5 (мВ/м) и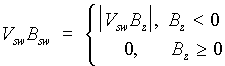 .
.
Интенсивность бури зависит не только от величины южной компоненты ММП, но и от длительности периода, в который ММП направлено на юг. Этот период определяет продолжительность главной фазы бури и, следовательно, глубину внедрения КТ в ловушку. Так, в результате статистического анализа 300 бурь показано, что для бурь с
max½ Dst½ > 100 нТ продолжительность главной фазы 14.0 ± 8.7 ч, а для бурь с max½ Dst½ < 50 нТ - 4.8 ± 3.5 ч [153].На основе уравнения (1) для одновременных спутниковых измерений полной энергии КТ и параметров солнечного ветра проводилось успешное моделирование вариаций
Dst во время разнообразных бурь [150, 153, 167, 168, 179, 180].В [168] показано, что величины
По виду буревых вариаций
Dst сделан вывод о связи между величинами t и Dst [45], что использовалось во многих работах. Однако в результате более полного анализа показано [168], что такая связь - вторична и возникает из-за корреляции Dst с VswBsw при достаточно больших значениях этих величин; если же рассматривать только данные, полученные при одинаковых значениях VswBsw , зависимость между t и Dst исчезает.При увеличении
VswBsw от 0 до 2 мВ/м параметр t уменьшается от ~ 18 до ~ 9 ч, а при дальнейшем увеличении VswBsw темп уменьшения t резко снижается и при VswBsw ~ 5¸ 11 мВ/м величина t очень слабо зависит от VswBsw , составляя ~ 4¸ 6 ч [168]. При VswBsw < 9 мВ/м зависимость t (VswBsw) хорошо аппроксимируется следующей функцией [168]: t (ч) = 2.4 exp {[9.74/[4.69 + VswBsw(мВ/м)]}. Для типичной умеренной бури VswBsw ~ 4 мВ/м и t ~ 8 ч [167, 168].Для описания буревых
Dst- вариаций применялось также нелинейное дифференциальное уравнение второго порядка [180], но это усложнение не даёт никаких преимуществ по сравнению с уравнением (1), дополненным эмпирической зависимостью t от VswBsw [168].Для объяснения эмпирической зависимости t
(VswBsw) в [168] рассматривалась модель, согласно которой VswBsw непрерывно контролирует положение КТ в ловушке и время жизни КТ определяется в основном перезарядкой. Однако в этой модели не учитывалось, что с увеличением электрического поля конвекции ионы КТ не только смещаются к Земле, но и ускоряются. Не учитывалась и зависимость сечения перезарядки от энергии частиц. С учётом этих обстоятельств при более глубокой инжекции ионов в ловушку уменьшения времени жизни за счёт перезарядки можно ожидать только для кислородного, азотного или углеродного КТ, а для протонного КТ это время должно увеличиваться (см. раздел 3.6). Но в модели [168] изменения ионного состава КТ во время бурь не рассматривались и полагалось, что основной вклад в энергию КТ вносят протоны.Что касается возможностей контроля VswBsw за положением КТ в ловушке, то это может относиться, по-видимому, только к главной фазе бури, а в [168] рассматривалась и фаза восстановления. В конце главной фазы, когда VswBsw и электрическое поле конвекции резко уменьшаются, значительная доля частиц, дрейфовавших по инфинитным траекториям, необратимо захватываются в ловушку и резкого смещения максимума КТ не происходит; на фазе восстановления бури внутренняя кромка КТ постепенно отодвигается от Земли "нос к носу" с плазмопаузой [4, 7, 11, 58].
Рассмотренный сценарий развития бурь основан на пересоединении межпланетного и магнитосферного магнитных полей. Эффективность такого пересоединения зависит от фаз вращения Земли вокруг оси и вокруг Солнца, что проявляется в сезонных вариациях геомагнитной активности: весной и осенью средний уровень геомагнитной активности выше, чем летом и зимой [181, 153]. Однако слабые и умеренные бури могут генерироваться и без пересоединения магнитных полей (модуляционные бури).
Вариации параметров солнечного ветра оказывают существенное влияние и на состояние ПС. Так, по данным ISEE-2 и ISEE-3 основные параметры ПС и солнечного ветра хорошо коррелируют друг с другом: концентрация солнечного ветра - с концентрацией ПС, скорость солнечного ветра - с температурой ПС, динамическое давление солнечного ветра - с давлением плазмы и полным давлением ПС и т.д. [79].
После учёта этих закономерностей зависимости параметров ПС от геомагнитной активности ослабляются и изменяются. Так, по данным ISEE-2 на r = 17.5¸ 22.5, абсолютные значения концентрации, температуры и давления ПС увеличиваются c ростом Kp, а при нормировании их на соответствующие параметры солнечного ветра концентрация и давление плазмы уменьшаются c ростом Kp и температура не зависит от Kp; эти выводы справедливы и на меньших r (вплоть до ГСО) и остаются в силе при переходе от Kp к AE [79].
Отсюда, казалось бы, можно заключить, что общей и единственной причиной изменения как уровня геомагнитной активности, так и характеристик ПС являются вариации параметров солнечного ветра. Однако установленные в [79] закономерности -
среднестатистические и получены без привязки начал суббурь к моментам резких изменений параметров солнечного ветра. При таком анализе причинно-следственные связи размываются: рассмотренные закономерности отражают лишь итоговый результат воздействия солнечного ветра на ПС. Непосредственная причина резких изменений того или иного параметра ПС обнаруживается только при более полном анализе данных.Так, факт нагревания ПС с ростом Kp обосновывался анализом данных методом наложения эпох с привязкой к началу суббурь [89] и если бы увеличение температуры ПС с ростом Kp зависело только от скорости солнечного ветра - следовало бы ожидать резкого изменения этой скорости перед началом суббури. Однако в действительности именно в момент начала суббури и в предшествующие ему десятки минут D Vsw минимально и не превышает десятых долей процента [79]. С другой стороны, начало суббури очень хорошо коррелирует с южной компонентой ММП в предшествующие этому началу 40 мин [79].
Важнейшим выводом проведённого здесь рассмотрения является следующий: взаимосвязи пространственно-энергетических распределений и ионного состава ближнего ПС магнитосферного хвоста, КТ и внешнего РП свидетельствуют о генетическом (а во многом и фактическом) единстве этих плазменных образований, что позволяют говорить о них как о единой системе и назвать её геокороной горячей плазмы.
Распределения ионных компонентов КТ и ближнего ПС термодинамически неравновесны. Вместе с тем, при m
/x i > 0.5 ± 0.2 кэВ/нТ инвариантные параметры и форма ионных спектров в геомагнитной ловушке и в ближнем ПС хорошо согласуются друг с другом, причём основные спектральные параметры горячей плазмы в ловушке можно связать со средними геометрическими и гидромагнитными параметрами ПС.Тесная связь КТ с ближним ПС проявляется во взаимосвязи бурь и суббурь: магнитная буря может развиваться и без суббуревого сопровождения, но в этом случае устойчивый захват частиц ПС в ловушку (необратимое переформирование и усиление замкнутого КТ) не реализуются; с другой стороны, буревая активность сильно влияет на суббуревую динамику ближнего ПС. Связи между КТ и ПС обеспечиваются общей магнитосферно-ионосферной системой токов и электрических полей.
Геокорона горячей плазмы является открытой диссипативной системой, которая описывается (строго) дифференциальными уравнениями в частных производных с нелинейными коэффициентами и откликается на внешние воздействия в зависимости от величины параметров, характеризующих ее собственное состояние. Такие уравнения допускают только численные решения. Компьютерное моделирование таких динамических систем на больших масштабах пространства и времени часто приводит к значительному расхождению получаемых решений при небольших изменениях свободных модельных параметров. Линеаризация же уравнений или параметризация (увеличение числа свободных параметров) системы, т.е. разбиение уравнения на искусственные кусочно-линейные участки, приводят к утрате очень важных, нетривиальных особенностей динамики системы, а иногда - даже к полному выхолащиванию её сущности.
С другой стороны, на фоне огромного многообразия, сложности и динамичности магнитосферных структур и процессов любые, даже самые подробные, экспериментальные данные, полученные одновременно на нескольких космических аппаратах с разными приборами, всегда имеют ограниченный, а из-за проблем, связанных с разделением пространственных и временных вариаций, - часто и весьма относительный характер. Поэтому тесный контакт экспериментальных и теоретических исследований в данной области - необходимое условие успеха и во многих случаях это единственный путь строго научного анализа. Экспериментальные результаты позволяют значительно упростить и конкретизировать важнейшие этапы математических расчетов, а теоретические разработки - систематизировать экспериментальные данные и внести в них необходимые поправки.
В последние 10- 15 лет в исследованиях горячей магнитосферной плазмы, особенно её ионного состава, получены очень значительные экспериментальные результаты. Разрабатываются очень интересные и глубокие теоретические подходы. Успешно развивается компьютерное моделирование. Изучены и получили убедительную количественную интерпретацию многие стационарные особенности пространственно-энергетических распределений горячей плазмы в планетарных магнитосферах. Однако мы всё ещё далеки от полного понимания механизмов протекающих здесь динамических процессов. Хотя многие детали магнитосферных процессов изучены достаточно хорошо, но целостной, однозначной и непротиворечивой количественной концепции явлений пока нет. В общей картине динамики магнитосферы пока нет чёткой иерархии различных физических процессов и механизмов: в различных областях магнитосферы и во время разных фаз геомагнитной активности относительные вклады различных процессов и взаимосвязи между ними могут значительно различаться.
1. Chapman S., Ferraro V. C. A new theory of magnetic storms // Nature. 1930. V. 126. P. 129- 130.
2. Frank L. A. On the extra-terrestrial ring current during geomagnetic storms // J. Geophys. Res. 1967. V. 72. P. 3753- 3768.
3. Frank L. A. Direct detection of asymmetric increases of extraterrestrial 'ring current' proton intensities in the outer radiation zone // J. Geophys. Res. 1970. V. 75. P. 1263- 1268.
4. Frank L. A. Relationship of the plasma sheet, ring current, trapping boundary, and plasmapause near the magnetic equator and local midnight // J. Geophys. Res. 1971. V. 76. P. 2265- 2275.
5. McIlwain C. E. Plasma convection in the vicinity of the geosynchronous orbit // in Earth's Magnetospheric Processes / Ed. B. M. McCormac / Norwell. Mass.: D. Reidel. 1972. P. 268- 279.
6. Smith P. H., Hoffman R. A. Ring current particle distributions during the magnetic storms of December 16- 18, 1971 // J. Geophys. Res. 1973. V. 78. P. 4731- 4737.
7. Smith P. H., Hoffman R. A. Direct observations in the dusk hours of the characteristics of the storm time ring current particles during the beginning of magnetic storms // J. Geophys. Res. 1974. V. 79. P. 966- 971.
8. Berko F. W., Cahill L. J., Jr., Fritz T. A. Protons as the prime contributions to storm time ring current // J. Geophys. Res. 1975. V. 80. P. 3549- 3552.
9. Lyons L. R., Williams D. J. Storm-associated variations of equatorially mirroring ring current protons, 1- 800 keV, at constant first adiabatic invariant // J. Geophys. Res. 1976. V. 81. P. 216- 220.
10. Smith P. H., Hoffman R. A., Fritz T. A. Ring current proton decay by charge exchange // J. Geophys. Res. 1976. V. 81. P. 2701- 2708.
11. Lyons L.R., Williams D. J. Quantitative Aspects of Magnetospheric Physics. Norwell. Mass.: D. Reidel. 1984.
12. Williams D. J. Dynamics of the Earth's ring current: Theory and observations // Space Sci. Rev. 1985. V. 42. P. 375- 396.
13. Kovtyukh A. S., Panasyuk M. I., Sosnovets E. N. et al. Enhancement of proton ring current during magnetic storms and local time asymmetry of low-latitude magnetic disturbances // Space Res. 1976. V. 16. P. 519- 522.
14. Лазарев В. И., Тверская Л. В., Тельцов М. В., Хорошева О. В. Асимметричная инжекция протонов кольцевого тока во время бури 6 июля 1974 г. // Геомагнетизм и аэрономия. 1977. Т. 17. С. 159- 161.
15. Ковтюх A. С., Панасюк М. И., Сосновец Э. Н. Сравнение потоков протонов малых энергий с критическими уровнями вблизи внешней границы радиационных поясов Земли // Космич. исслед. 1977. Т. 15. С. 102- 108.
16. Ковтюх А. С., Панасюк М. И., Сосновец Э. Н. Магнитный эффект асимметричного кольцевого тока протонов // Космич. исслед. 1977. Т. 15. С. 559- 565.
17. Ковтюх А. С., Панасюк М. И., Сосновец Э. Н. Динамика протонов кольцевого тока во время бури 25. I. 1974 г. // Космич. исслед. 1978. Т. 16. С. 226- 237.
18. Fennell J. F., Johnson R. J., Young D. T. et al. Plasma and electric field boundaries at high and low altitudes // J. Geophys. Res. 1982. V. 87. P. 5933- 5942.
19. Geiss J., Balsiger H., Eberhardt P. et al. Dynamics of magnetospheric ion composition as observed by the GEOS mass spectrometer // Space Sci. Rev. 1978. V. 22. P. 537- 566.
20. Balsiger H., Eberhardt P., Geiss J., Young D. T. Magnetic storm injection of 0.9- to 16 keV/e solar and terrestrial ions into the high-altitude magnetosphere // J. Geophys. Res. 1980. V. 85. P. 1645- 1662.
21. Young D. T., Balsiger H., Geiss J. Correlations of magnetospheric ion composition with geomagnetic and solar activity // J. Geophys. Res. 1982. V. 87. P. 9077- 9096.
22. Козелова Т. В., Лазутин Л. Л. Инжекция протонов на 6.6 RE в ранние вечерние часы и связанные с ней явления // Геомагнетизм и аэрономия. 1994. Т. 34. С. 37- 44.
23. Lundin R., Lyons L. R., Pissarenko N. Observations of the ring current composition at L < 4 // Geophys. Res. Lett. 1980. V. 7. P. 425- 428.
24. Lundin R., Hultqvist B., Pissarenko N., Zakharov A. Composition of the hot magnetospheric plasma as observed with the Prognoz-7 satellite // Energetic Ion Composition in the Earth's Magnetosphere / Ed. R. G. Johnson / Tokyo. Terra Sci. 1983. P. 307- 351.
25. Sharp R. D., Johnson R. G., Lennartsson W. et al. Hot plasma composition results from the ISEE 1 spacecraft // Energetic Ion Composition in the Earth's Magnetosphere / Ed. R. G. Johnson / Tokyo: Terra Sci. 1983. P. 231- 261.
26. Lennartsson W. Energetic (0.1- to 16 keV/e) magnetospheric ion composition at different levels of solar F10.7 // J. Geophys. Res. 1989. V. 94. P. 3600- 3610.
27. Johnson R. G., Strangeway R. J., Shelley E. G. et al. Hot plasma composition results from the SCATHA spacecraft // Energetic Ion Composition in the Earth's Magnetosphere / Ed. R. G. Johnson / Tokyo: Terra Sci. 1983. P. 287- 306.
28. Mauk B. H., Meng C.-I. Macroscopic ion acceleration associated with the formation of the ring current in the Earth's magnetosphere // Ion Acceleration in the Magnetosphere and Ionosphere / Geophys. Monogr. Ser. V. 38. Ed. T. Chang / Washington. AGU. 1986. P. 351- 361.
29. McEntire R. W., Lui A. T. Y., Krimigis S. M., Keath E. P. AMPTE/CCE energetic particle composition measurements during the September 4, 1984 magnetic storm // Geophys. Res. Lett. 1985. V. 12. P. 317- 320.
30. Shelley E. G., Klumpar D. M., Peterson W. K. et al. AMPTE/CCE observation of the plasma composition below 17 keV during the September 4, 1984 magnetic storm // Geophys. Res. Lett. 1985. V. 12. P. 321- 324.
31. Klecker B., Mö bius E., Hovestadt D. et al. Discovery of energetic molecular ions (NO+ and O2+) in the storm time ring current // Geophys. Res. Lett. 1986. V. 13. P. 632- 635.
32. Gloeckler G., Hamilton D. C. AMPTE ion composition results // Phys. Scripta. 1987. V. T18. P. 73- 84.
33. Lui A. T. Y., McEntier R. W., Krimigis S. M. Evolution of the ring current during two geomagnetic storms // J. Geophys. Res. 1987. V. 92. P. 7459- 7470.
34. Sibeck D. G., McEntire R. W., Lui A. T. Y. et al. Magnetic field drift shell splitting: Cause of unusual dayside particle pitch angle distributions during storms and substorms // J. Geophys. Res. 1987. V. 92. P. 13,485- 13,497.
35. Hamilton D. C., Gloeckler G., Ipavich F. M. et al. Ring current development during the great geomagnetic storm of February 1986 // J. Geophys. Res. 1988. V. 93. P. 14,343- 14,355.
36. Kistler L. M., Ipavich F. M., Hamilton D. C. et al. Energy spectra of the major ion species in the ring current during geomagnetic storms // J. Geophys. Res. 1989. V. 94. P. 3579- 3599.
37. Lui A. T. Y., McEntier R. W., Sibeck D. G., Krimigis S. M. Recent findings on angular distributions of dayside ring current energetic ions // J. Geophys. Res. 1990. V. 95. P. 20,839- 20,851.
38. Kremser G., Wilken B., Gloeckler G. et al. Origin, transport, and losses of energetic He+ and He++ ions in the magnetosphere of the Earth: AMPTE/CCE observations // Ann. Geophys. 1993. V. 11. P. 354- 365.
39. Chen M. W., Lyons L. R., Schulz M. Simulation of phase space distributions of storm time proton ring current // J. Geophys. Res. 1994. V. 99. P. 5745- 5759.
40. Christon S. P., Hamilton D. C., Gloeckler G. et al. High charge state carbon and oxygen ions in Earth's equatorial quasi-trapping region // J. Geophys. Res. 1994. V. 99. P. 13,465- 13,488.
41. Fok M.-C., Moore T. E., Kozyra J. U. et al. Three-dimensional ring current decay model // J. Geophys. Res. 1995. V. 100. P. 9619- 9633.
42. Jordanova V. K., Farrugia C. J., Janoo L. et al. October 1995 magnetic cloud and accompanying storm activity: Ring current evolution // J. Geophys. Res. 1998. V. 103. P. 79- 92.
43. Kozyra J. U., Fok M.-C., Sanchez E. R. et al. The role of precipitation in producing the rapid early recovery phase of the Great Magnetic Storm of February 1986 // J. Geophys. Res. 1998. V. 103. P. 6801- 6814.
44. Kamide Y., Baumjohann W., Daglis I. A. et al. Current understanding of magnetic storm: Storm-substorm relationships // J. Geophys. Res. 1998. V. 103. P. 17,705- 17,728.
45. Daglis I. A., Thorne R. M., Baumjohann W., Orsini S. The terrestrial ring current: Origin, formation, and decay // Rev. Geophys. 1999. V. 37. P. 407- 438.
46. Greenspan M. E., Hamilton D. E. A test of Dessler-Parker-Sckopke relation during magnetic storms // J. Geophys. Res. 2000. V. 105. P. 5419- 5430.
47. Власова Н.А., Ковтюх А.С., Панасюк М.И. и др. Ионный кольцевой ток во время магнитных возмущений по наблюдениям на геостационарной орбите. 2. Вариации энергетических и зарядовых спектров ионов во время умеренных бурь // Космич. исслед. 1988. Т. 26. С. 746- 752.
48. Власова Н. А., Ковтюх А. С., Панасюк М. И. и др. Ионный кольцевой ток во время магнитных возмущений по наблюдениям на геостационарной орбите: 3. Вариации ионного состава во время слабых магнитных возмущений // Космич. исслед. 1988. Т. 26. С. 881- 889.
49. Власова Н.А., Ковтюх А.С., Панасюк М.И. и др. Взаимосвязь пространственных, угловых и энергетических распределений частиц на геостационарной орбите // Космич. исслед. 1989. Т. 27. С. 94- 101.
50. Власова Н.А., Ковтюх А.С., Панасюк М.И. и др. Суточные вариации и энергетические спектры ионов кольцевого тока на геостационарной орбите // Космич. исслед. 1989. Т. 27. С. 411- 418.
51. Ковтюх А.С., Власова Н.А. Корреляция потоков электронов и ионов кольцевого тока с индексами геомагнитной активности и параметрами межпланетной среды // Геомагнетизм и аэрономия. 1996. Т. 36. С. 1- 12.
52. Daglis I. A., Axford W. I., Livi S. et al. Auroral ionospheric ion feeding of the inner plasma sheet during substorms // J. Geomagn. Geoelectr. 1995. V. 48. P. 729- 739.
53. Gazey N. G., Lockwood M., Grande M. et al. EISCAT/CRRES observations: Nightside ionospheric ion outflow and oxygenrich substorm injections // Ann. Geophys. 1996. V. 14. P. 1032- 1043.
54. Wolf R. A., Freeman J. W., Jr., Hausman B. A. et al. Modeling convection effects in magnetic storms // Magnetic Storms / Eds. B. Tsurutani et al. / Geophys. Monogr. Ser. V. 98. Washington: AGU. 1997. P. 161.
55. Chen M. W., Roeder J. L., Fennell J. F. et al. Simulations of ring current proton pitch angle distributions // J. Geophys. Res. 1998. V. 103. P. 165- 178.
56. Rowland D., Wygant J. R. Dependence of the large-scale, inner magnetospheric electric field on geomagnetic activity // J. Geophys. Res. 1998. V. 103. P. 14,959- 14,964.
57. Wygant J. R., Rowland D., Singer H. J. et al. Experimental evidence on the role of the large spatial scale electric field in creating the ring current // J. Geophys. Res. 1998. V. 103. P. 29,527- 29,544.
58. Burke W. J., Maynard N. C., Hagan M. P. et al. Electrodynamics of inner magnetosphere observed in the dusk sector by CRRES and DMSP during the magnetic storm of June 4- 6, 1991 // J. Geophys. Res. 1998. V. 103. P. 29,399- 29,418.
59. Chen M. W., Roeder J. L., Fennell J. F. et al. Proton ring current pitch angle distributions: Comparison of simulations with CRRES observations // J. Geophys. Res. 1999. V. 104. P. 17,379- 17,389.
60. Ковтюх А.С., Мартыненко Г.Б., Сосновец Э.Н. Суточный ход энергетических спектров ионов H+, He2+ и О+ кольцевого тока на геостационарной орбите по данным ИСЗ "Горизонт-35" // Космич. исслед. 1995. Т. 33. С. 455- 462.
61. Ковтюх А.С., Мартыненко Г.Б. Вариации жёсткости спектров солнечного и ионосферного компонентов ионов кольцевого тока // Космич. исслед. 1995. Т. 33. С. 599- 607.
62. Ковтюх А.С., Мартыненко Г.Б. Корреляция вариаций потоков ионов многокомпонентного кольцевого тока с Kp- индексом // Космич. исслед. 1996. Т. 34. С. 3- 14.
63. Ковтюх А.С. Резонанс ионов кольцевого тока с дрейфовыми волнами // Космич. исслед. 1998. Т. 36. С. 142- 155.
64. Ковтюх А.С., Мартыненко Г.Б., Сосновец Э.Н., Смирнов М.Ю. Особенности динамики энергетических спектров ионного кольцевого тока во время сильных бурь // Космич. исслед. 1998. Т. 36. С. 369- 375.
65. Ковтюх А.С., Власова Н.А., Павлов Н.Н. и др. Суббуревые вариации потоков и энергетических спектров протонов в диапазоне 0.1- 133 кэВ на геостационарной орбите // Космич. исслед. 1999. Т. 37. С. 463- 469.
66. Jordanova V. K., Farrugia C. J., Quinn J. M. et al. Simulation of off-equatorial ring current ion spectra measured by Polar for a moderate storm at solar minimum // J. Geophys. Res. 1999. V. 104. P. 429- 436.
67. Ghielmetti A. G., Johnson R. G., Sharp R. D., Shelley E.G. The latitudinal, diurnal, and altitudinal distributions of upward flowing energetic ions of ionospheric origin // Geophys. Res. Lett. 1978. V. 5. P. 59- 62.
68. Ma Sung L. S., Gloeckler G., Fan C. Y., Hovestadt D. Observations of the mean ionization states of energetic particles in the vicinity of the Earth's magnetosphere // J. Geophys. Res. 1980. V. 85. P. 5983- 5991.
69. Lui A. T. Y., Krimigis S. M. Earthward transport of energetic protons in the Earth's plasma sheet // Geophys. Res. Lett. 1981. V. 8. P. 527- 530.
70. DeCoster R. L., Frank L. A. Observations pertaining to the dynamics of the plasma sheet // J. Geophys. Res. 1979. V. 84. P. 5099- 5121.
71. Peterson W. K., Sharp R. D., Shelley E.G. et al. Energetic ion composition of the plasma sheet // J. Geophys. Res. 1981. V. 86. P. 761- 767.
72. Takahashi K., Hones E. W., Jr. ISEE 1 and 2 observations of ion distributions at the plasma sheet - tail lobe boundary // J. Geophys. Res. 1988. V. 93. P. 8558- 8582.
73. Williams D. J., Mitchell D. G., Frank L. A., Eastman T. E. Three dimensional plasma ion distribution from 200 eV to 2 MeV // J. Geophys. Res. 1988. V. 93. P. 12,783- 12,794.
74. Lennartsson W. A scenario for solar wind penetration of Earth's magnetic tail based on ion composition data from the ISEE 1 spacecraft // J. Geophys. Res. 1992. V. 97. P. 19,221- 19,238.
75. Huang C. Y., Frank L. A. Magnitude of Bz in the neutral sheet of the magnetotail // J. Geophys. Res. 1994. V. 99. P. 73- 82.
76. Lennartsson W. Tail lobe ion composition at energies of 0.1 to 16 keV/e: Evidence for mass-dependant density gradient // J. Geophys. Res. 1994. V. 99. P. 2387- 2401.
77. Baker D. N., Pulkkinen T. I., Hesse M., McPherron R. L. A quantitative assessment of energy storage and release in the Earth’s magnetotail // J. Geophys. Res. 1997. V. 102. P. 7159- 7168.
78. Lyons L. R., Huang C. Y. Plasma sheet expansion on r = 15- 22 RE: A recovery phase or expansion phase phenomenon? // J. Geophys. Res. 1994. V. 99. P. 10,995- 11,004.
79. Borovsky J. E., Thomsen M. F., Elphic R. C. The driving of the plasma sheet by the solar wind // J. Geophys. Res. 1998. V. 103. P. 17,617- 17,630.
80. Goslin J. T., McComas D. J., Phillips J. L., Bame S. J. Geomagnetic activity associated with Earth passage of interplanetary shock disturbances and coronal mass ejections // J. Geophys. Res. 1991. V. 96. P. 7831- 7839.
81. Heikkila W. J. Comment on “A quantitative assessment of energy storage and release in the Earth’s magnetotail” D. N. Baker, T. I. Pulkkinen, M. Hesse, and R. L. McPherron // J. Geophys. Res. 1998. V. 103. P. 17,729- 17,732.
82. Krimigis S. M., Haerendel G., Gloeckler G. et al. AMPTE lithium tracer releases in the solar wind: Observations inside the magnetosphere // J. Geophys. Res. 1986. V. 91. P. 1339- 1353.
83. Lopez R. E., Lui A. T. Y., Sibeck D. J. et al. On the relationship between the energetic particle flux morphology and the change in the magnetic field magnitude during substorms // J. Geophys. Res. 1989. V. 94. P. 17,105- 17,119.
84. Kistler L. M., Mö bius E., Klecker B. et al. Spatial variations in the suprathermal ion distributions during substorms in the plasma sheet // J. Geophys. Res. 1990. V. 95. P. 18,871- 18,885.
85. Daglis I. A., Livi S., Sarris E. T., Wilken B. Energy density of ionospheric and solar wind origin ions in the near-Earth magnetotail during substorms // J. Geophys. Res. 1994. V. 99. P. 5691- 5703.
86. Mö bius E., Scholer M., Klecker B. et al. Acceleration of ions of ionospheric origin in the plasma sheet during substorm activity // Magnetotail Physics / Ed. A. T. Y. Lui / Baltimore. Md.: Johns Hopkins Univ. Press. 1987. P. 231- 234.
87. Baumjohann W., Pascmann G., Luhr H. Characteristics of high-speed ion flows in the plasma sheet // J. Geophys. Res. 1990. V. 95. P. 3801- 3809.
88. Nakamura M., Pascmann G., Baumjohann W., Scopke N. Ion distributions and flows near the neutral sheet // J. Geophys. Res. 1991. V. 96. P. 5631- 5649.
89. Kistler L. M., Baumjohann W., Nagai T., Mö bius E. Superposed epoch analysis of pressure and magnetic field configuration changes in the plasma sheet // J. Geophys. Res. 1993. V. 98. P. 9249- 9258.
90. Baumjohann W., Kamide Y., Nakamura R. Substorms, storms, and the near-Earth tail // J. Geomagn. Geoelectr. 1996. V. 48. P. 177- 185.
91. Fairfield D. H., Mukai T., Lui A. T. Y. et al. Geotail observations of substorm onset in the inner magnetotail // J. Geophys. Res. 1998. V. 103. P. 103- 117.
92. Wilken B., Zong Q.-G., Doke T. et al. Substorm activity on January 11, 1994: Geotail observations in the distant tail during the leading phase of a corotating interaction region // J. Geophys. Res. 1998. V. 103. P. 17,671- 17,689.
93. Nosé N., Lui A. T. Y., Ohtani S. et al. Acceleration of oxygen ions of ionospheric origin in the near-Earth magnetotail during substorms // J. Geophys. Res. 2000. V. 105. P. 7669- 7677.
94. von Steiger R., Geiss J., Gloeckler G. et al. Magnesium, carbon and oxygen abundances in different solar wind flow types, as measured by SWICS on ULYSSES // Solar Wind 7 / Eds. E. March and R. Schwenn / New York: Pergamon. 1992. P. 399- 403.
95. Frank L. A., Patterson W. R., Kivelson M. G. Observations of nonadiabatic acceleration of ions in Earth's magnetotail // J. Geophys. Res. 1994. V. 99. P. 14,877- 14,890.
96. Тактакишвили А. Л., Зеленый Л. М., Луценко В. Н., Кудела К. О спектрах энергичных частиц в хвосте магнитосферы Земли // Космич. исслед. 1998. Т. 36. С. 282- 291.
97. Ермолаев Ю. И., Петрукович А. А., Зеленый Л. М. и др. Исследования структуры и динамики плазменного слоя в эксперименте КОРАЛЛ проекта ИНТЕРБОЛ // Космич. исслед. 2000. Т. 38. С. 16- 22.
98. Ковтюх А.С. Использование магнитосферы в качестве анализатора формы спектров частиц радиационных поясов // Геомагнетизм и аэрономия. 1984. Т. 24. С. 566- 570.
99. Ковтюх А.С. О форме энергетического спектра протонов радиационных поясов Земли и механизмах его формирования // Геомагнетизм и аэрономия. 1985. Т. 25. С. 886- 892.
100. Ковтюх А.С. Двухмаксимумная пространственно-энергетическая структура внешнего радиационного пояса ионов // Геомагнетизм и аэрономия. 1989. Т. 29. С. 26- 32.
101. Ковтюх А.С. Солнечно-циклические вариации инвариантных параметров энергетических спектров ионов радиационных поясов Земли // Космич. исслед. 1999. Т. 37. С. 57- 69.
102. Ковтюх А.С. О механизмах формирования инвариантных параметров и скейлинге ионных спектров в геомагнитной ловушке // Космич. исслед. 1999. Т. 37. С. 231- 244.
103. Ковтюх А.С. Суббуревая динамика основных параметров и механизмы формирования ионных спектров кольцевого тока // Космич. исслед. 2000. Т. 38. С. 42- 53.
104. Garrett H. B. Review of quantitative models of the 0- to 100-keV near-Earth plasma // Rev. Geophys. Space Phys. 1979. V. 17. P. 397- 417.
105. Ковтюх А.С. Соотношения вкладов ионосферного и солнечного источников ионов в кольцевой ток и плазменный слой геомагнитосферы: Новый метод анализа // Космич. исслед. 2000. Т. 38. С. 233- 243.
106. Ковтюх А.С. Соотношения вкладов ионосферного и солнечного источников ионов в кольцевой ток и плазменный слой геомагнитосферы: Анализ экспериментальных данных новым методом // Космич. исслед. 2000. Т. 38. С. 347- 362.
107. Ковтюх А.С. Связь питч-угловых и энергетических распределений ионов радиационных поясов Земли // Геомагнетизм и аэрономия. 1993. Т. 33. № 4. С. 52- 62.
108. Ковтюх А.С., Башкиров В.Ф. Питч-угловые распределения ионов радиационных поясов Земли. 1. Стационарная модель для области дипольного магнитного поля // Геомагнетизм и аэрономия. 1994. Т. 34. № 2. С. 9- 19.
109. Башкиров В.Ф., Ковтюх А.С. Питч-угловые распределения ионов радиационных поясов Земли: 3. Математическая модель для реального магнитного поля // Геомагнетизм и аэрономия. 1994. Т. 34. № 2. C. 29- 37.
110. Башкиров В.Ф., Ковтюх А.С. Стационарные питч-угловые распределения протонов радиационных поясов Земли в области сильной диссипации // Геомагнетизм и аэрономия. 1995. Т. 35. № 4. С. 8- 21.
111. Башкиров В.Ф., Ковтюх А.С. Динамика питч-угловых распределений ионов кольцевого тока и радиационных поясов во время главной фазы бури // Геомагнетизм и аэрономия. 1995. Т. 35. № 5. С. 56- 62.
112. Chen M. W., Schulz M., Lyons L. R., Gorney D. J. Stormtime transport of ring current and radiation belt ions // J. Geophys. Res. 1993. V. 98. P. 3835- 3849.
113. Galperin Yu. I., Feldstein Ya. I. Auroral luminosity and its relationship to magnetospheric plasma domains // Auroral Physics / Eds. C.-I. Meng et al. / New York: Cambridge Univ. Press. 1991. P. 207- 222.
114. Tverskoy B. A. Electric fields in the magnetosphere and the origin of trapped radiation // Solar-Terrestrial Physics / Ed. E. R. Dyer / Dordrecht. Holland: D. Reidel. 1970. P. 297- 317.
115. Green J. L., Horwitz J. L. Desting of Earthward streaming plasma in the plasmasheet boundary layer // Geophys. Res. Lett. 1986. V. 13. P. 76- 79.
116. Pashalidis N. P., Sarris E. T., Krimigis S. M. et al. Energetic ion distributions on both sides of the Earth's magnetopause // J. Geophys. Res. 1994. V. 99. P. 8687- 8703.
117. Chen J., Fritz T. A., Sheldon R. B. et al. Cusp energetic particle events: Implications for a major acceleration region of the magnetosphere // J. Geophys. Res. 1998. V. 103. P. 69- 78.
118. Chappell C. R., Moore T. E., Waite J. H., Jr. The ionosphere as a fully adequate source of plasma for the Earth’s magnetosphere // J. Geophys. Res. 1987. V. 92. P. 5896- 5910.
119. Mä lkki A., Lundin R. Altitude distributions of upward ion beams and solitary wave structures on the Viking data // Geophys. Res. Lett. 1994. V. 21. P. 2243- 2246.
120. Hultqvist B. On the acceleration of positive ions by high-latitude large-amplitude electric field fluctuations // J. Geophys. Res. 1996. V. 101. P. 27,111- 27,121.
121. Andre M., Koskinen H., Matson L. Local transverse ion energization in and near the polar cusp // Geophys. Res. Lett. 1988. V. 15. P. 107- 110.
122. Shelley E. G. Initial hot plasma composition results from Dynamic Explorer // in Energetic Ion Composition in the Earth's Magnetosphere / Ed. R. G. Johnson / Tokyo: Terra Sci. 1983. P. 353- 367.
123. Chiu Y. T., Cladis J. B., Frances W. E. Simulation of ion heating in the topside auroral ionosphere // Geophys. Res. Lett. 1988. V. 15. P. 1534- 1537.
124. Moore T. E. Modulation of terrestrial ion escape flux composition (by low-altitude acceleration and charge exchange chemistry) // J. Geophys. Res. 1980. V. 85. P. 2011- 2016.
125. Ghielmetti A. G., Shelley E.G., Klumpar D. M. Correlation between number flux and energy of upward flowing ion beams // Phys. Scripta. 1987. V. 36. P. 362- 366.
126. Cattell C. A., Nguyen T., Temerin M. et al. Effects of solar cycle on auroral particle acceleration // Auroral Plasma Dynamics / Geophys. Monogr. Ser. V. 80. / Washington: AGU, 1993. P. 219- 226.
127. Cannata R. W., Gombosi T. I. Modeling of the solar cycle dependence of quiet-time ion upwelling at high geomagnetic latitudes // Geophys. Res. Lett. 1989. V. 16. P. 1141- 1144.
128. Collin H. L., Sharp R. D., Shelley E.G. The magnitude and composition of the outflow of energetic ions from the ionosphere // J. Geophys. Res. 1984. V. 89. P. 2185- 2194.
129. Reitt W. J., Schunk R. W. Composition and characteristics of the polar wind // in Energetic ion composition in the Earth's magnetosphere / Ed. R. G. Johnson / Tokyo: Terra Sci. 1983. P. 99- 141.
130. Nagai T., Waite J. H., Jr., Green J. L. et al. First measurements of supersonic polar wind in the polar magnetosphere // Geophys. Res. Lett. 1984. V. 11. P. 669- 672.
131. Yau A. W., Shelley E.G., Peterson W. K., Lenchyshyn L. Energetic auroral and polar ion outflow at DE 1 altitudes: Magnitude, composition, magnetic activity dependence, and long-term variations // J. Geophys. Res. 1985. V. 90. P. 8417- 8432.
132. Speiser T. W., Williams D. J., Garcia H. A. Magnetospherically trapped ions as a source of magnetosheath energetic ions // J. Geophys. Res. 1981. V. 86. P. 723- 732.
133. Chen J., Palmadesso P. J. Chaos and nonlinear dynamics of single-particle orbits in a magnetotaillike magnetic field // J. Geophys. Res. 1986. V. 91. P. 1499- 1508.
134. Bü chner J., Zelenyi L. M. Deterministic chaos in the dynamics of charged particles near a magnetic field reversal // Phys. Lett. 1986. V. A118. P. 395- 399.
135. Bü chner J., Zelenyi L. M. Regular and chaotic charged particle motion in magnetotaillike field reversals, 1, Basic theory of trapped motion // J. Geophys. Res. 1989. V. 94. P. 11,821- 11,842.
136. Zelenyi L. M., Lominadze J. G., Taktakishvili A. L. Generation of energetic proton and electron bursts in the planetary magnetotail // J. Geophys. Res. 1990. V. 95. P. 3883- 3891.
137. Delcourt D. C., Sauvaud J.-A. Generation of energetic proton shells during substorms // J. Geophys. Res. 1991. V. 96. P. 1585- 1599.
138. Delcourt D. C., Sauvaud J.-A., Martin R. F., Jr., Moore T. E. On the nonadiabatic precipitation of ions from the near-Earth plasma sheet/ // J. Geophys. Res. 1996. V. 101. P. 17,409- 17,418.
139. Lyons L. R., Speiser T. W. Evidence for current sheet acceleration in the geomagnetic tail // J. Geophys. Res. 1982. V. 87. P. 2276- 2286.
140. Zelenyi L. M., Lipatov A. S., Lominadze D. G., Taktakishvili A. L. The dynamics of the energetic proton bursts in the course of the magnetic field topology reconstruction in the Earth’s magnetotail // Planet. Space Sci. 1984. V. 32. P. 313- 324.
141. Lui A. T. Y., Lopez R. E., Anderson B. J. et al. Current disruptions in the near-Earth neutral sheet region // J. Geophys. Res. 1992. V. 97. P. 1461- 1480.
142. Harel M. R., Wolf R. A., Spiro R. W. et al. Quantitative simulation of a magnetospheric substorm, 2, Comparison with observations // J. Geophys. Res. 1981. V. 86. P. 2242- 2260.
143. Tverskoy B. A. Main mechanisms in the formation of the Earth's radiation belts // Rev. Geophys. 1969. V. 7. P. 219- 232.
144. Sauvaud J.-A., Beutier T., Delcourt D. On the origin of flux dropouts near geosynchronous orbit during the growth phase of substorms. 1. Betatron effects // J. Geophys. Res. 1996. V. 101. P. 19,911- 19,919.
145. Sá nchez E. R., Mauk B., Meng C.-I. Adiabatic vs. nonadiabatic particle distributions during convection surges // Geophys. Res. Lett. 1993. V. 20. P. 177- 180.
146. Wodnicka E. B., Banaszkiewicz M. The features of the auroral topside ionosphere- magnetosphere coupling induced by the time-dependent magnetic field // Adv. Space Res. 1996. V. 18. P. 233- 236.
147. Liu W. W., Rostoker G. Energetic ring current particles generated by recurring substorm cycles // J. Geophys. Res. 1995. V. 100. P. 21,897- 21,911.
148. Sugiura M., Poros D. J. A magnetospheric field model incorporating the OGO 3 and 5 magnetic field observations // Planet. Space Sci. 1973. V. 21. P. 1763- 1773.
149. Золотухина Н. А., Полех Н. М., Рахматулин Р. А., Харченко И. П. Среднеширотные геомагнитные пульсации в бурю 18-19 октября 1995 г. Геомагнетизм и аэрономия. 1999. Т. 39. № 1. С. 47- 54.
150. Ebihara Y., Ejiri M. Modeling of solar wind control of ring current buildup: A case study of the magnetic storms in April 1997 // Geophys. Res. Lett. 1998. V. 25. P. 3751- 3754.
151. Chen M. W., Lyons L. R., Schulz M. Stormtime ring-current formation: A comparison between single- and double-dip model storms with similar transport // J. Geophys. Res. 2000. V. 105. P. 27,755- 27,765.
152. Gonzalez W. D., Tsurutani B. T., Gonzalez A. L. C. et al. Solar wind-magnetosphere coupling during intense magnetic storms (1978- 1979) // J. Geophys. Res. 1989. V. 94. P. 8835- 8851.
153. Kamide Y., Yokoyama N., Gonzalez W. D. et al. Two-step development of geomagnetic storms // J. Geophys. Res. 1998. V. 103. P. 6917- 6921.
154. Baumjohann W., Haerendel G., Melzner F. Magnetospheric convection observed between 0600 and 2100 LT: Variations with Kp // J. Geophys. Res. 1985. V. 90. P. 393- 398.
155. Зверев В. Л., Пудовкин М. И., Старков Г. В. Движение сияний и электрические поля на предварительной фазе суббури // Геомагнетизм и аэрономия. 1994. Т. 34. № 2. С. 49- 55.
156. Stern D. P. Large-scale electric fields in the Earth's magnetosphere // Rev. Geophys. 1977. V. 15. P. 156- 194.
157. Nishida A. Formation of a plasmapause, or magnetospheric plasma knee by combined action of magnetosphere convection and plasma escape from the tail // J. Geophys. Res. 1966. V. 71. P. 5669- 5679.
158. Cambou F., Galperin Yu. I. Main results of the joint French-Soviet space project ARCAD-1 and ARCAD-2 for magnetospheric, auroral and ionospheric physics // Ann. Geophys. 1982. V. 38. P. 87- 110.
159. Usadi A., Wolf R. A., Heinemann M., Horton W. Does chaos alter the ensemble-averaged drift equations? // J. Geophys. Res. 1996. V. 101. P. 15,491- 15,514.
160. Кропоткин А. П. Об эволюции потоков энергичных частиц при их инжекции в магнитосферу // Геомагнетизм и аэрономия. 1977. Т. 17. С. 259- 266.
161. Alexeev I. I., Belenkaya E. S., Kalegaev V. V. et al. Magnetic storms and magnetotail currents // J. Geophys. Res. 1996. V. 101. P. 7737- 7747.
162. Dessler A. J., Parker E. N. Hydromagnetic theory of geomagnetic storms // J. Geophys. Res. 1959. V. 64. P. 2239- 2252.
163. Sckopke N. A general relation between the energy of trapped particles and the disturbance field near the Earth // J. Geophys. Res. 1966. V. 71. P. 3125- 3130.
164. Шабанский В. П. Явления в околоземном пространстве. М.: Наука. 1972.
165. Langel R. A., Estes R. H. Large-scale, near-field magnetic fields from external sources and the corresponding induced internal field // J. Geophys. Res. 1985. V. 90. P. 2487- 2494.
166. Sckopke N. A study of self-consistent ring current models // Cosmic Electrodyn. 1972. V. 3. P. 330- 348.
167. Burton R. K., McPherron R. L., Russell C. T. An empirical relationship between interplanetary conditions and Dst // J. Geophys. Res. 1975. V. 80. P. 4204- 4214.
168. O'Brien T. P., McPherron R. L. An empirical phase space analysis of ring current dynamics: Solar wind control of injection decay // J. Geophys. Res. 2000. V. 10. P. 7707- 7719.
169. Maltsev Y. P., Arykov A. A., Belova E. G. et al. Magnetic flux redistribution in the storm-time magnetosphere // J. Geophys. Res. 1996. V. 101. P. 7697- 7704.
170. Antonova E. E., Ganushkina N. Yu. Azimuthal hot plasma pressure gradients and dawn-dusk electric field formation // J. Atmos. Solar-Terr. Phys. 1997. V. 59. P. 1343- 1354.
171. Antonova E. E. Plasma pressure distribution in the inner magnetosphere and the applicability of Dessler-Parker-Sckopke relation to storm time magnetic disturbance description // Adv. Space Res. 2000. V. 25. P. 2357- 2360.
172. Antonova E. E., Ganushkina N. Yu. Inner magnetosphere current and their role in the magnetospheric dynamics // Phys. Chem. Earth (C). 2000. V. 25. P. 23- 26.
173. Антонова Е. Е. Радиальные градиенты давления в магнитосфере Земли и величина Dst-вариации // Геомагнетизм и аэрономия. 2001. Т. 41. С. 148- 156.
174. Tsyganenko N. A. Modeling the magnetosphere: The asymmetric ring current and Region 2 Birkeland currents revisited // J. Geophys. Res. 2000. V. 105. P. 27,739- 27,754.
175. Sö raas F., Davis L.R. Temporal Variations of the 100 keV to 1700 keV Trapped Protons observed on Satellite Explorer 26 during First Half of 1965 // GSFC Rep. X- 612- 68- 328. Greenbelt. Md.: Goddard Space Flight Center. 1968.
176. Blake J. B., Kolasinski W. A., Fillius R. W., Mullen E. G. Injection of electrons and protons with energies of tens of MeV into L < 3 on March 24, 1991 // Geophys. Res. Lett. 1992. V. 19. P. 821- 824.
177. McIlwain C. E. Ring current effects on trapped particles // J. Geophys. Res. 1966. V. 71. P. 3623- 3628.
178. Ковтюх А.С. Методы выделения адиабатической составляющей в буревых вариациях потоков ионного кольцевого тока // Космич. исслед. 2002. Т. 40.
179. Feldstein Y. I. Modeling of the magnetic field of magnetospheric ring current as a function of interplanetary medium parameters // Space Sci. Rev. 1992. V. 59. P. 83- 165.
180. Vassiliadis D., Klimas A. J., Valdivia J. A., Baker D. N. The Dst geomagnetic response as a function of storm phase and amplitude and the solar wind electric field // J. Geophys. Res. 1999. V. 104. P. 24,957- 24,976.
181. Russell C. T., McPherron R. L. Semiannual variation of geomagnetic activity // J. Geophys. Res. 1973. V. 78. P. 92- 108.


|
Copyright (c) by SiZiF Co, НИИЯФ МГУ 2002.
Для связи:
lll@srd.sinp.msu.ru